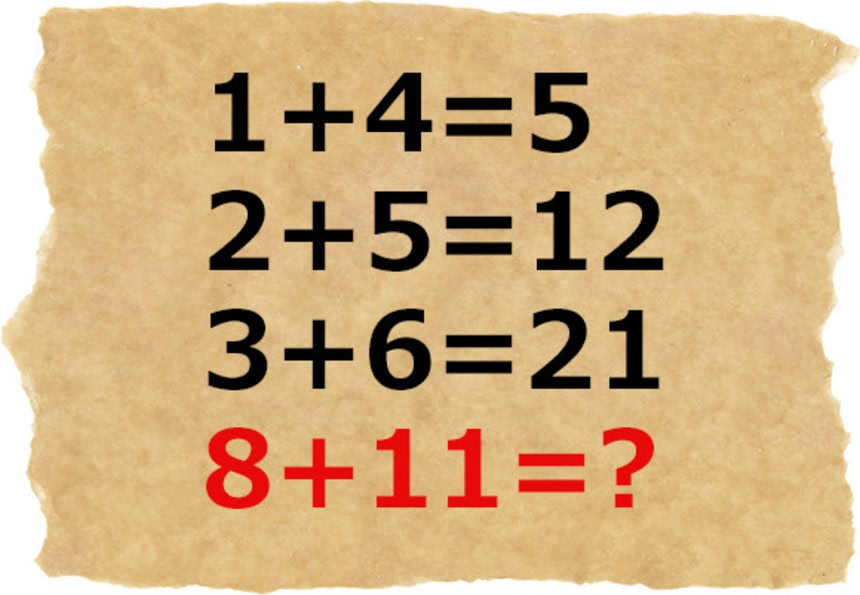この画像を大きなサイズで見るSNSで定期的に話題となり、拡散される計算クイズがある。
毎回様々なキャッチコピーがつけられているが、この答が2つあるというクイズ、前回話題になったのは2年前で、その時のキャッチコピーは「両方の答えにたどり着ける人は1000人に1人」だった。
同じ問題ながら今回は「両方わかるとIQ130以上」となっていた。
2年後に再びバズるというのはそれだけ面白い問題なのだろう。ということで前に紹介しているが、初見という人はやってみよう。
これはただの足し算ではなく頭の体操、クイズであり、2つの法則があてはまるのだそうだ。両方の答えを見つけることができるかな？
答えは2つ。隠れた法則をつきとめよう
実はこの問題、ネット上ではたびたび話題となっているものなので、既に知っている人も多いかもしれない。とりあえず問題を見ていこう。
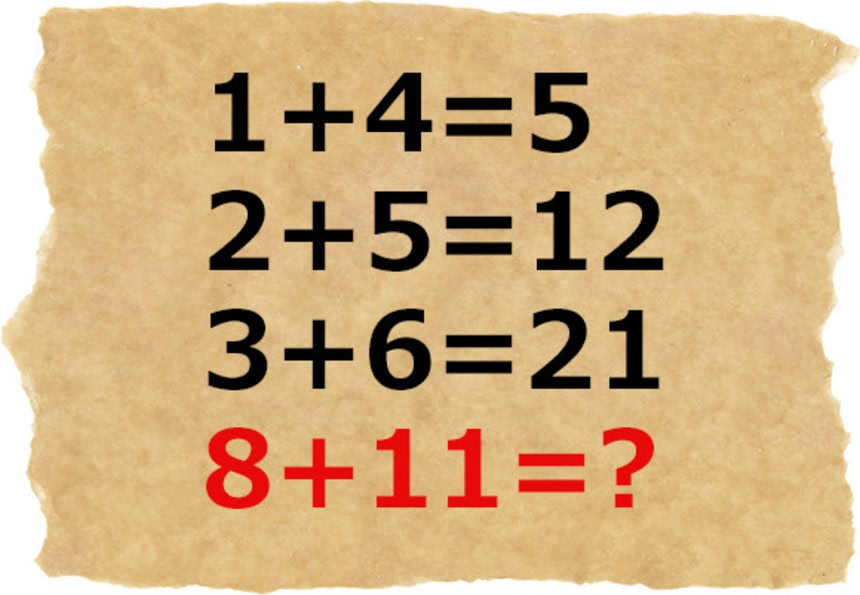この画像を大きなサイズで見る上の数式には共通の法則が隠されている。一連の式が数学的に成り立つようにして「？」の答えを求めてみよう。
答えは2つ。また、一連の式にあてはまる法則は2種類あり、それぞれに1つずつ別の答えがある。なお、サイトではIQ130以上の人なら両方わかるとあるが、これといった根拠はないらしい。
さてどうだろう？
両方の答えを見つけた人もいるかな？
それじゃあ2つの解答をしていこう。
解答1
これは多くの人がたどり着きそうな解答だ。
各式を穴埋め式の足し算とみなし、右辺の数から逆算する。すると1番上の式は左辺に0（画像では省略）、2番目は5、3番目は12を加える数式となる。
この画像を大きなサイズで見るこの時点で各式の右辺と同じ数が、すぐ下の左辺に加えられていることに気づけば、4番目の左辺に加えるのは3番目の右辺の21だとわかる。
よって21+8+11=40
答えは40だ。
解答2
こちらの答えはちょっとひらめきが必要になるかもしれない。
1～3番目の左辺を項ごとに上から眺めると、最初の項が1、2、3 、次の項が4、5、6、と連続している。だが、4番目は4+7にはならず、3番目の各項に4を加えた8+11になっている。
そこで3番目から4番目の式の間に、各項の数が1つずつ増える数式が4つ隠されているとみなせば、以下のようになる。
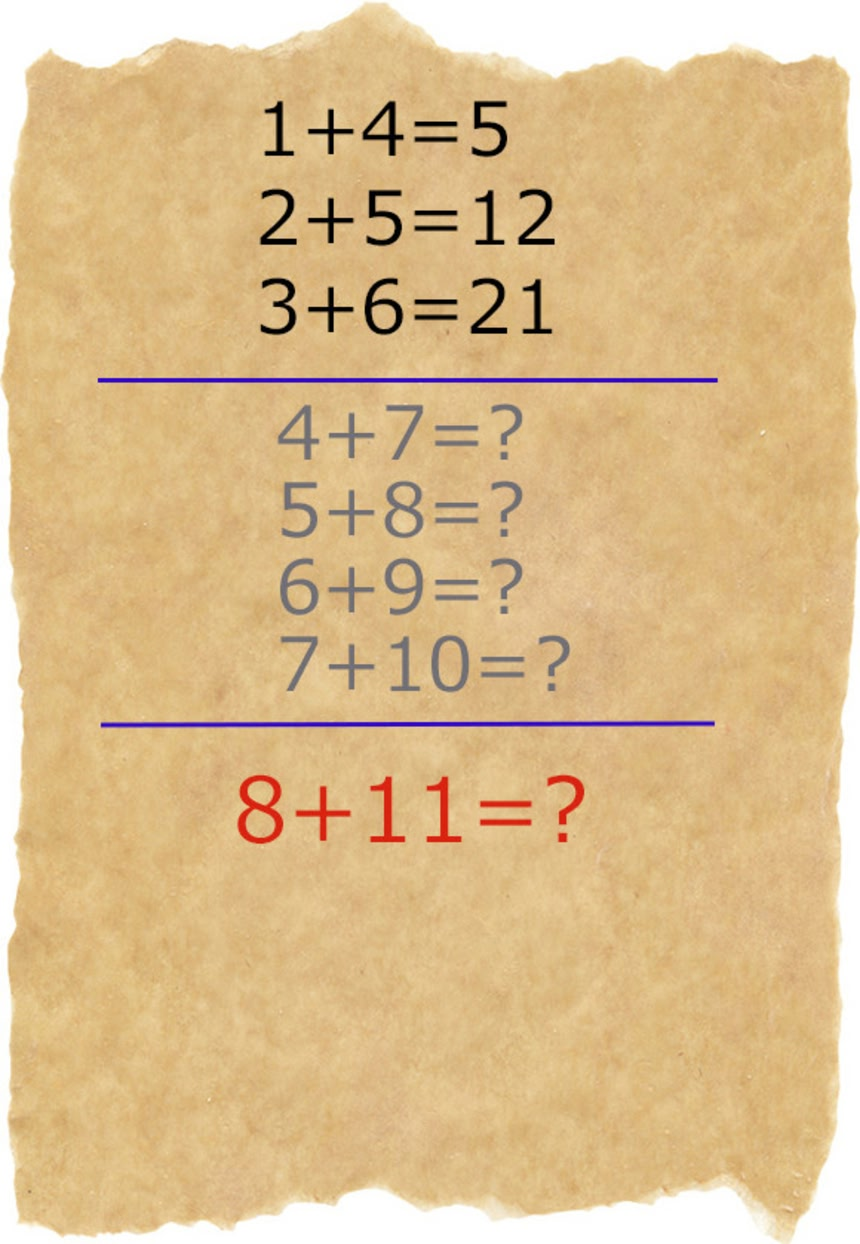この画像を大きなサイズで見るそこから、解答1のように一つ上の式の右辺の数が、下の左辺に加えられる法則を当てはめると、8番目(元4番目)の左辺に加えるのは7番目の右辺の77になる。
この画像を大きなサイズで見るよって77+8+11=96
答えは96だ。
てことで、みんなどうだった？
知能指数はさておき、式のあちこちに着目して色々な法則を考えてると思考の柔軟性が上がる気がするぞ。
あと、すぐにピンと来て2つの法則をきっちり見つけた人も、見つけたつもりで違ってた！って人も、ちょっとした気分転換になったんじゃないかな？
References:theepochtimesなど /written by D/ edited by parumo
一目で二つの回答が判った。
つか、これが判らなかったという人は多分ボケッとしていただけだと思う。
※1
それがパッとわかるかわからないのかってのがIQの違いって事よ
わからない人は「普通に」いる
それが理解できない人はIQは高くてもコミュニケーション能力は低いかも
※1
第三の解
各行の右辺が
6進法
5進法
4進法
なので3進法の 201
40が導き出せた時点で大喜びしてしまった自分…
※2
自分もそうでした（ー▽ー）
>>2
答えは52だよね…？だよね？
こういうの大嫌い。だって+ってのは足すことを支持してる記号なのに、それを別の使い方するわけでしょ？+って書かずに◆とか何らかの別の記号であらわすべきじゃない？
それなら並び方から法則を見出すのはいくらでもやってもいいと思うけど。
40と96両方分かったけど96の出し方違ったわ
※3
わかる
表とかで問題出してほしい
※3
それを言うなら悪いのは＋じゃなくて＝のほうだと思う。
＋はちゃんと自分の仕事はしている様子。
あと掛け算を持ち出して答えを導いてる人は確かにIQ高そうだけど、
設問者の示したルール「＋」を完全に無視しているという点で
設問に対する解法としては正解と言えるのかどうか微妙な気がする。
※3
こういうのが好きな人に言わせると、
記号のミスリードもクイズのうちなんだってさ。
＋というただの文字なのか、加算記号なのか、取捨選択する手間も頭の体操になる。
◇とかにしてしまうと、問題が簡単になってしまう。
※3の人と同意見
回答1はすぐ分かったけど2は出て来なかったな。
こういう部分的に伏せておいて最終的に法則性が～みたいな
推理小説になれなかったミステリー小説染みたこじつけありきの問題は
出題者の底意地の悪さしか感じられない
>>3
わからなかったんだね…
閃きのほうだけしかパッと浮かばなかった自分とは…変人(ﾟДﾟ;)
2の方しかわからんかった しかもやり方が違う
答え96の方が導き方が二つあるからなんともなあ
>>6
自分も96は導いたがやり方が違った
>>81
そう！掛け算が交じるんだよね
最初に96が浮かんで、答えは2つと聞いてちょっと考えて40が浮かんだ
どちらも正解でスッキリ～
悩んでたら〇＋△=Xが
〇＋〇×△=Xだなって思って
1+1×4=5
2+2×5=12
3+3×6=18
てことは
8+8×11だから96か…って思ってたら
答えだけあってて出し方が違った
※8さんの解き方しか気付かなかったけど
頭が固いって蔑まれてもいいや
>>8
コメントで出てる答えは、数式にすると
a=n*(n+3)+n=n^2+4n
(aが答え、nは1,2,3…)
解答2はbを答えとすると
b=(1+4)+(2+5)+(3+6)+…+(n+3+n)
=(1+2+3+…+n)*2+3n
1+2+…+nの和は高校で習う公式で
(1+n)*n/2 となるから
={(1+n)*n/2}*2+3n
=m^2+4n
=a
つまり数式の形が違うだけで、計算方法は同じ
>>44
解答は両方すぐ分かったけど、
こんな難しいプロセスじゃなかった…
論理的な能力ってすごいっすね。
96の方が先に出たけど、掛け算方式で考えてた
40の方は……解き方はわかったけど
21+8をなぜか31にしてしまったので、答えが42になったｗ
※44と※68さんのおかげで解2も掛け算方式も同じだとわかって納得した
ちゃんと数式で説明できるってすごい
※8
自分もこれで出しましたが、解答2の方法は
A + Bを計算するときに前の答えが(A – 1) x Bだと(最初は(1-1)xB=0より成立)
(A – 1) x B + A + B = A + A x Bで
解答2の解法 = ※8の解法なので実質同じことを計算しているんですよね。
>>8
俺もこれだった
※8
自分もこの解き方してたって書こうとしたら同じ人沢山いて笑った
まあ普通なのかな
>>8
自分もどっちもわかったけどこの式で出してた。と思ったら44が解説してくれた。頭いい人って答えがわかるからじゃなくて、納得させられるからすごいんだと思うわ。
答えは96になったが、法則2には当てはまらなかった…
解き方は、左辺の2つの数値を掛けた後に、左辺の1つ目の数値を足すやり方
「1+4=5」なら、1×4+1
「2+5=12」なら、2×5+2
「3+6=21」なら、3×6+3
「8+11=?」なら、8×11+8 で “96”といった感じ
※9
私もこれでした
※9
私もそう思った
これじゃダメなのかな
※9
俺も。
12と21がそれぞれ2の段と3の段にあるよなーって思ってたらすぐに浮かんだ。
逆に解答2のしか思い浮かばんかった…
1+4=5は1＋1×4=5、2+5=10は2＋2×5=10、3+6=21は3＋3×6=21って感じにできるな
ってことで8＋11は8＋8×11=96って数字が出てきた
左辺と右辺とを掛けた数に左辺を足せば２番目の解と同じになる
左右の数字を掛けた答えに、左の数字を足したものだと思った
２つとも解は合ってるけど違う方法でたどり着いた
これってある意味ハズレだよね
a+b=c として
答えがいつも ax(b+1)になってるので
８+１１は ８ｘ（11+1）で96
どの行も左辺の2つの数字を掛け合わせて何行目かの数字を足しているのだから
4行目は8×11＋4で92
も正解になるの？
※15
先生を困らせるタイプの天才
>>15
これでもいいでしょ
オレは全然分からなかったけど解答２は＋を×にして最初の数字を足すと同じ答えになるのはどーして？
※16
回答2も＋を×にして最初の数字を足すのも数式的には同じだから。
96はわかったけど逆に40の出し方があっさり過ぎて合ってるか疑っちゃったわ
1＋4→1+1×4＝5
2＋5→2＋2×5＝12
3＋6→3＋3×6＝21
だから、
8＋11→8＋8×11＝96
結局正解は同じになるけど、こっちの方がシンプルじゃない？
>>18
そうそう！
左の数字は縦に1.2.3で、右は4.5.6。
その合計の数字は左右の掛け算に左の数字を足したもの。
ああ、a+b→cとして、ab+a→cってことね
…これ以外出てこなかった。なんじゃコレ
2だけ5秒くらいで気が付いたのに1に最後まで気がつけなかった私・・・
屁理屈
自分だけの適当なひらめきでルールを作る事など誰でも出来る
それを「解ればIQ○○」など見当違い甚だしい
以上の理由でクイズ・なぞなぞ・パズルは作るのは簡単、答えるのは難しい
74と24だ！と思って大爆死
三歩譲ってその式だけで完結するなら良いが
独立した前の式からなんか持ってくるのは気に入らんな
まぁ答え自体は10秒も有れば出るわ
>>25
普通やらないね
さらにあくまでプラス記号にこだわるなら
n進数で上から6543という手もある
答えは61
笑
>>37
間違えた答えは201
>>58
答え見たら進数についての物がなかったので書いてくれてる人がいて助かりました！
勘違いかと思い込むところでした…
二つわかりました。一つ目は
１＋４✖１＝５ ２＋５✖２＝１２ ３＋6✕３＝２１ ……８＋11✕８＝９６
これは、左辺の第一項の数字を第二項の数字にかけて、その数字に第一項を足す。
二つ目は左辺のすべての数字を足す。
（１＋４）＋（２＋５）＝１２
（１＋４）＋（２＋５）＋（３＋６）＝２１
（１＋４）＋（２＋５）＋（３＋６）＋（４＋７）＋（５＋８）＋（６＋９）＋（７＋１０）＋（８＋１１）＝９６
1+4*1=5
2+5*2=12
3+6*3=21
8+11*8=96
こんなん簡単やろって思ったら間違えて
4掛けてずっと？？ってなった
「穴埋式の足し算」てーのがそもそも考えにない。
悪問にしか見えない。
1+(1×4)=5
2+(2×5)=12
3+(3×6)=21
8+(8×11)=96
1×(4+1)=5
2×(5+1)=12
3×(6+1)=21
8×(11+1)=96
本当にIQが高いのは「52」と答えた人です。
コメント欄でドヤ顔している人たちは全員凡人。
間違った情報を鵜呑みにしないようにしましょう。
え？IQ130以上？ご冗談をｗｗｗ
一番目の回答はおかしい。一行目と二行目の式に関連性は無いから。
1+4＝5
2+5＝12
3+6=21
7＋10=17
8+11=36
9+12=57
の方がしっくりくるんだけどな
これなら両方の法則を使っても答えは同じで36
でもまあ、間違えたか
掛け算をして左側の数字を足すのが答えだと思った。それでも96って正解にたどり着けた
答えだけ書けば正解
式を書けば間違い
96はa*b+aで出した
パズルとしてはいいんだけど、計算の記号使うのはどうなんだろうな
見た瞬間96って思った。IQ130はウソだなｗ
96はすぐわかって、しばらく睨めっこして40もわかった。
と思ったら96は解き方違った・・・。
既に出てるけど8×11＋8のやりかた。
１２３４５６という数字が出ていることを考えると、
たしかに全部足す方法が正しいですね。
そもそも問題が足し算だし。
記事とコメで発想の違いがあるのは
日本人はほぼ全員暗算で掛け算ができるからなんだと思う
96は瞬間的に出て来たけど
40は発想自体無かったな。
なぞなぞかと思ってた。
1+4=5を1回目として、n回目の行はn(n+4)だから、n=8なら8(8+4)=96と出たよ。
「解けたら◯◯」とか「あなたのIQがわかる！」みたいなやつはついついやっちゃう。
そして解いた後に必ず「いやいや、こんなんで分かるワケねー」って思うまでがデフォなんだけどね。
でもやっちゃうわね。
1×(4+1)=5
2×(5+1)=12
3×(6+1)=21
8×(11+1)=96
と言う、わけのわからない導き出し方をしてしまった。
※50
式が違うだけで8×11+8と同じですよ
これ以外にも共通として見いだせる式があったらそれも正解
2つしかないというのが間違い
なんか解答1って、解答2にたどり着く前に誤答として消去するものだと思うんだが…
規則性を考えたら2しか正解だとは思わないなあ
計算式で回答を導くタイプと、直感で「ああ、そういうことね」って答えを出しちゃうタイプに分かれるね
自分は直感型
わーい両方とけたー。
でも俺も、96のほうは、8×11+8だった。
説明どおりの解き方をした人のほうがむしろ少ないんじゃないかなあ？
俺も96で出してしまったな
答えみて40の方が簡単だったと思ったわ
そして２つ答えがあるという文を読んでいなかった
これ答えれたら130は嘘だな
多分もっと低くても答えれる
3つの解法（解は2つ）をみつけたけど、「＋」を和算でなくするやり方を正とするのなら、使用している「１」や「２」や「3」などの文字だって、ほかの数字に置き換えたり、数字じゃない記号や、数字と記号の組み合わせに変換できちゃうわけで、そうするともっと、”正解とされるもの”は生み出せるだろうね。面倒なので考えてないが(-_-;)
答え１は間違った導き方と思います。なぜならば連番としか考えられないでしょう
答え２の数字に2通りの回答があるので此方のみ正解では無いでしょうか？
1+4=5 〇
2+5=12 ×
3+6=21 ×
もう少し頑張りましょう
「a+b=c として答えがいつもax(b+1)になっている」というコメントがあるけれど、この解法がいちばん論理的。
また「元の問題で＋の記号を用いているのがおかしい」という指摘もまったく当然。なにか別の記号を用いるべき。
そうした疑問を抱かずに用意された回答を「へ～、そうなんだ」と鵜呑みにするのはいただけませんね。
頭の中でパズルができるかどうかじゃない？
想像力がないと試行錯誤が出来ない
解こうと思ったけど途中でめんどくさくなって回答だけ見た奴は俺だけじゃないはず
うーんこれはウソだ、そんなに頭良くないし、自分
間に…のような中略がないので、96は回答として成立しないように思う。
8+11=は、4番目になるので回答としては52が正解でないとおかしいようにしか見えないわ。
40は一瞬だったけど96は少し考えたよ
出し方はやっぱり8×11＋8になっちゃったなあ
どっちも出てすっきり＾＾
皆が書いてるように8×11でやった
真の天才は19と答える
※71
上におかしな数式があるからと言って答えが変わるわけじゃないしね
しかし「答えが2つという」前提があるから19だけでは不十分。
もう1つの答えは811。
解答1も2も1番上だけ書いてある通りに計算するのがどうしても気持ち悪い。
a*b+aが一番スッキリしてていい。解答通りに思いつけなきゃIQ高くないってんならおらぁバカでいいや
２つの解法が分かって初めてI.Q130で
１つなら凡人って事なのかな？
以前WAIS3受けたけど2日くらい掛かって初めて
I.Qが分かる様だったので、本当に知りたい方は専門機関へどうぞ。
どっちも分かんなかった！╰(*´︶`*)╯
二つ目が最初にわかったけど、二通りあると言われなければ一つ目には絶対にたどり着けなかった
両方分かったけど、前者は法則成り立ってなくね？って思って別の答え探してしまったわ。
別に数学の問題じゃないしありなんだろうが、しっくりこない。
>>76
確かに後者は法則成り立って答えが出るけど、
前者は123から8に飛んでるのに、足すだけ良いのかってなってしまう。
それが許されるなら後者8+11*4=52って
答えた人も正解でいい様な気がする。
なんだかんだいろんな計算法で
解いているみなさんが
単純にすごいと思う！
1+4=5 =1×5
2+5=12 =2×6
3+6=21 =3×7
8+11=64=8×8
>>80
8×12=96
一分以内で両方の回答方法と答えがわかってしまった
自分の才能が恐い(ガクガクブルブル
>>82
天才かな、親から貰ったその才能を斜内に役立てるんだ
結論：問題が悪い（負け惜しみ）
猛烈に野暮なことを言う人がいるなｗ
そもそも2+5=12を良しとする事にひっかかる
謎解きだからと言われればそれまでですが
なぞなぞとかパズルってのは作者の意図を暴く作業だから、知性を匂わすために宇宙の法則やらを持ち込んでも逆に滑稽だよ
凡人であることを受け入れる勇気を持とう
一個しかわからんかった
直ぐわかって、出来た。自分でもビックリ。
そんな私は高卒。あんまIQ関係ないみたい～
IQ130くらいならそこら辺にいっぱいいる説
両方かけて左側を足すのかと思ったけど、全然違くてがっかり
8*11+8で96じゃないの
なんにせよ出題者の想定が甘いからなあ
a*b+a=c
っていう法則があるじゃん
a+b=c
(a+1)+(b+1)=dとして
①a×(b+1)=cのパターン
②a×b+a=cのパターン
両方で96にたどり着ける
40になるパターンは連続性無視ってことかい
1+4=5 (6進数)
2+5=12 (5進数)
3+6=21 (4進数)
8+11=201(3進数)
これが一番しっくりくる
※96
しゅごい・・・
89だが？
左右の数字を掛けて右の数字を足すと答えになる
もう一つ上に答えが0になる計算があって答えが上の答えに+5、+7、+9になって+2ずつ増えてくと考えたんだけどどうだろう…
ＩＱ１３０とかじゃなく単に「脳のリラックス度」を測る指針では
自分でも解けたしｗ
解答1は「このはし渡るな」って書いてあったら真ん中歩く人
まず問題の意味がわかりません(´･∀･`)
ちげーよ！
二つ目の数字を一つ目は1倍二つ目は2倍三つ目を三倍にして足すと答えが出る。
てめえら知能が低いんだよ（笑）
>>102
かけ算入っとるやん
わかったけどせいぜい110くらいじゃない？
他のコメントで出てるかもしれないけど
A+B=C だとして、
1+4=5
2+5=12
3+6=21
はA×B+Aの法則で導けた
だから8+11=?は
8×11+8で96
あっちのほうはインテリジェンスなんです。
1+(1×4)=5
2+(2×5)=12
3+(3×6)=21
8+(8×11)=96
で96に辿り着いたけど、これは後者と一緒？
※108と同じく、最初の数を後ろの数にかけて答えを出した
１+４=５
の間に
１+（１×）４=５
２+５=12
の間に
２+（２×）５=12
という感じにして答えと符合するようにした
どちらの答えも出せたけど、96は違う解き方をしてしまった。
1×4+1=5
2×5+2=12
↓
8×11+8=96
あと、40の法則で間に書いてない4～7も順に計算して行ったら、96になったよ。
なんで？(笑)
最近頭良くなったと思ってたら、２つともわかった
やっぱり頭良くなってたんだなぁ
72と96か？
96はすぐ分かったけど、40なるほど。
1 + 4 = 5 (6進法） / 2 + 5 = 12 (5進法) / 3 + 6 = 21 (4進法)
式三つセットで+の左側1→3、右側4→6だから次の三つは
7 + 10 / 8 + 11 / 9 + 12
と予測して真ん中は19を5進法で表して34とかオカルティックなこと考えてた。
なぜ○進法が6,5,4のサイクルかは謎。
ギリシャ数字とか手で指折り数えたんだと思ったわ
1+4は手を開いて「5」
2+5は手「V」とピースサイン分多くて「II」で「VII」12
3+6は手の2個分「X」より「I」少なくて「IX」21
8+11は手の4個分「XX」より「I」少なくて「IXX」41とか考えてたわ
編みかけの掛け算でとけるよね？
左の数字×下の問題の右側にある数字を掛け算すれば、上の問題の答えになる
1+4=5 1×5
2+5=12 2×6
3+6=21 3×7
4+7=32 4×8
5+8=45 5×9
6+9=60 6×10
7+10=77 7×11
8+11=96 8×12
9+12=117 9×13
コメント数が答えを抜いた・・・
唐突に
1+ 4 →１（４＋１）＝5
2+ 5 →２（５＋１）＝12
3+ 6 →３（６＋１）＝21
8+11→８（11＋1 ）＝96
と思いついたんだけど、こういうのはダメなの？
a＋b＝c
d＋e＝f
e×a＝c
ブヒー
1+1*4=5
2+2*5=12
3+3*6=21
8+8*11=96
だと思った
2の方合ってたけど解き方違うわ
奇数の数字を足してやってた
1＋4＝5
2＋5＝12（＋7）
3＋6＝21（＋9）
4＋7＝32
中略
8＋11（＋19）＝96
数学は苦手だけど両方わかった。
隠された式なんて言い出したら、いくらでも答えを増やせるが…。
解答1の方はちょっと無理やり感ある
こういう出題だと1個ずつの数式は独立していて、それぞれを満たす共通の法則を探してしまうね
両方直ぐに分かったけど130は大袈裟だと思う
小学生の頃調べた自分の知能指数は105位だったから
当てはまる法則は２つと断言しているけど、探せば無限にあるんじゃないかなあ。
回答書かなきゃ良いのに
IQだけは高いんだけどなぁ、、
積算されてゆくってのは判ったんだけど実際に計算スルの面倒…
だったんだけど自分の考えて計算したら答えは96で合っていた。
すっごい単純だけど私の思いついた方法は余りに面倒くさい物だった…
（1から8までを足した物)＋(4から11までを足した物）
2番の方がすぐに思い浮かんだ
1番の方は答え見てもよくわかんない
自分は片方だけ解けた。96のほう。 だが、これは家でじっくり考える時間があったからで、こんなの嬉しくもなんともない。紙とペンと時間があるんだから解けて当然ちゃ当然なので自慢にもならない。
こういうの解けたからっ
て得意げになったり、解けなかった人を上から目線でどうこういうのはよくないね。
そういうのはＩＱ以前にＥＱが低すぎる。
あとさ、解けるか解けないかは、手もとに何か書くものがあるかどうかによるよね。
電車の中でスマホで見てる人と家でＰＣの前にいる人とではだいぶ差が出る。
紙とペンこそ至高の思考道具だからね。
昨今じゃ紙とペンを携帯するなんてスマホ偏重の世の中で嗜好品化しつつあるけど。
40と92だと思った..
1 1+4=5
2 2+5=12(解の差は12-5で7)
3 3+6=21(解の差は21-12で9)
ときたので
はー、前の解との解同士の差は2ずつ広がっていくんやね
んじゃ 前の解+(前の解の差+2）やね
で2は解いたやね
んで1は思いつかんかった
法則でいうなら
足し算を掛け算に変えて
一番前の数を足せば答えになる
1×4+(1)=5
2×5+(2)=12
3×6+(3)=21
4×7+(4)=32
5×8+(5)=45
6×9+(6)=60
7×10+(7)=77
8×11+(8)=96
〇×(△+1)はおらんのか
規則性の中から92を見出した人も評価して欲しい
何でか分からないけど普通に分かっちゃった
96が出せたのに40が出なかったのは
きっと俺だけではないはず。
謎解き系のゲームばっかりやってるのですぐわかった。頭が多少は柔らかくなってるのかな。
サムネイルの時点で法則はわかった
結構ひらめいた人多いと思う
4×1+1=5
5×2+2=12
6×3+3=21
11×4+8=52
これだめなの？？
足し算を掛け算に直して左の数字を足しても出るよね？
１１×８に最初の１１を足すというのは違うのか？
上はその法則なんだけども
2つ目もう1つ出来上がるよね
○+△＝□ は
○+（○×△）＝□
になるね
むしろこっちかなって思ったよ
1*(4+1)=5
2*(5+1)=12
3*(6+1)=21
8*(11+1)=96
じゃだめなの？
後者の答はすぐわかったけど、前者の方は数分かかった。
学校の試験が全てIQテストなら楽だったんだが、理系科目でさえも記憶偏重だしなぁ。
この国でIQ高くてもほとんどメリット無いのが実感。
2が面白いのは、1の解き方ができるなら２もできるという事。
やってることは同じで、ただ工程が増えただけだもの。2桁の足し算のやり方を習ったなら、習わずとも20桁でも200桁でも足し算ができるのと同じ。ただ掛け算とか近道する方法を覚えてからだと、このやり方は考え付きにくいだろうな。
あのなあバカども、有限個の数列からはいくらでも一般項が作れるんだからな。
答えは2つではなく無限に作れるぞ。
※157
バカはあんたでしょう？文章よく読めよｗ読解力もIQの一部だぞ。
答えを二つ見つければﾞ…って書いてるだろ。
解法を「数」を求められてはいない。
求められているのは「2通りの解法を提示すること」5個も6個も答え方は求められていないよ。2つだけ見つけろって書いてんのよ。1個でも3個でもない、「2つ」見つければいい。それだけのこと。余計なことはしなくていいんだよ。
つかさぁ、経験則なんだけど他人をバカ扱いするやつほど馬鹿なんだよね。
これって売り言葉に買い言葉じゃなくて、マジでそうなんだよ。
劣等感の塊のくせに、プライドが高くて自分が賢いと思い込んでて常に人を見下してて、
普段は雄弁なんだけど自分より賢い人間が現れると急に黙り込んじゃうタイプ。君がそうなんじゃないの？
怪盗１が分からんのに怪盗２を２通りの出し方で正当できた
しかも２通りとも書いてるのと違う方法で
なんじゃこれ
どっちもわかったけど、俺はIQは130もない。絶対ないｗ
40はわかったけどもう一個のほうが普通に説いただけだった
①a*(b+1) で 96
②(a+1)*b-3 で 96
の２つかと思った。
３つの例式は全てa+3=bが成り立っているので①＝②になるけど。
45と96を出した人、
自分以外にいませんか……
計算は苦手だけどクイズ番組とかでよくあるパターンを試したら解けた。
だから解けた人はIQ130というのは大げさだと思う。
逆に数学得意で頭が良い人のほうが答えに納得いかない！！（怒）
になる問題っぽいね。
大学で数列式と線形代数を習えば普通に導けると思うんだが、こんなのIQ関係なく、高校の数学以降に応用数理を学んだかどうかじゃないの？
無理矢理法則を作ればもっとあるだろうしIQ関係ないねこれ
すぐ解けた50歳調理師だけど、掛け算の方。
足し算や、何進法とか考えるのが時間がかかるな。
国際ネットＩＱテストより簡単や
1＋(4×1)＝5 →1行目だから
2＋(5×2)＝12 →2行目だから
3＋(6×3)＝21 →3行目だから
8＋(11×4)＝52 →4行目だから
とか思って自信満々に答えを見たら違ったー凡人には思い付かぬわ二つ目。
９６の方は２通りの出し方があるよね。
A1+B1=C1
A2+B2=C2
以下・・・として、
A１xB１＋A１＝C1 って方法
もう一つは
A1ｘB2＝C1
１５分くらいで解けたけど、こんなもん小学生でもわかると思うけど、
答えが２つあるってのは導き方なのか？に当てはまる数字なのか先に言ってくれなきゃ
２個目の解き方を思いついた時点で考えるのを止めちゃうわ。
両方を２分で説いた
まあIQ８０なんだけどな
これは簡単すぎだな
30秒と掛からずに2通り分かった
自分はIQ130も無いよ
答えが２通りあるって知らされてなければ別だけど
IQ130は２通りあることを知らずに２通りの答えがすぐに出せる人だね
かんちがいしてた
1+4=5→1+4*1=5
2+5=12→2+5*2=12
3+6=21→3+6*3=21
8+11=？→8+11*8=96
だと思ってたw
40はすぐわかったけどなー。
40はトンチかって分かってこれを数字足して間さを足して96は思い付かなかった・・・w
92だろ。
イエーい、メンサの皆んな見てる〜？
ちゃんとした計算式になってないとダメなのか。
なぞなぞとして解いたら全然違う答えになったよｗ
解答2はすぐわかりました。同じく96になる解き方で、上左と下右の数字をかけ算しても96が導き出せる。
1×5=5
2×6=12
3×7=21
4×8=32
5×9=45
6×10=60
7×11=77
8×12=96
これは第三の計算法則になりませんかね?
解けて草
パッと答えがわかって「やべ、俺天才かも」って思ったらほとんどみんなわかってて凡人に成り下がった(ﾟωﾟ)
※186
.いや、多分違う。
わからなかった人は、わからなかったことが恥ずかしいから書き込まないだけ。
わかった人だけが、「俺、スゲーだろ。誰かこの問題わかっちゃう俺を認めてッ！」みたいな気分の高揚の高まったときに勢いに任せて書き込んでるだけだから。 わからない人も相当数いるし、片方だけ…って人もまた相当数いる。
80も答えになる
答えは3つある
（プラスの左の数字）×（プラスの右の数字＋１）かなと思って答えは96
もう一つはわからなかったので解説を読んだが解説が何言ってるのかがわからない
141はちがうのか
見たら分かるとか10秒で解けたとか絶対盛ってるだろ
いやまあコメントの解説見てるだけで頭が割れそうになるくらい数学苦手で、これも解が96になるのしか解けなかった人間の僻みなんだけどさ（5分以上はかかったと思う）
解が複数存在する時点で、テストとしてはどうなのか・・・
この、二つ目の解法
1+4=5
1(4
二つ目の答えの96には他にも解法がある
1+4=5
1×(4+1)=5
2+5=12
2×(5+1)=12
3+6=21
3×(6+1)=21
8+11=96
8×(11+1)=96
こんなの、どうでしょう？
ひと目で2個わかってもよくて108ぐらいだね
簡単すぎ
答えは96になったけど考え方が全然違ったw
右に1足して左とかけた
後者の答えは出せたけど40っていうのは閃かなかったなぁ
アホなのは21+4+7を33って計算してて1ズレてたこと
96は一瞥して思いついた
8×11+8=96
「もう１つは算術で扱うモノではないはずだ」
「大体、クイズって書いてあるし」
「左辺に出てくる数字は最大で11、これは１月～１２月を表しているのだろうか？」
「いや、数字を英語読みした場合のアルファベットとか？もしくは画数？」
「数字をデジタル表示したときの何か？使われない部位とか？」
「いや、数字ですらなくて図形として扱うべきか？どこかに線を引くと対象な図形になるとか・・・」
この辺で自分が迷宮に入ってしまった事だけはわかった
答えを見た
くそう、、、思いっきり算術じゃねえか！
思い込みって良くないな・・・って同じ境遇のヒトいない？
96の導き方2つって意味じゃないの？
俺はそう理解して答え出したけど
解答1はちょっと違う気がするよ
（A1）複数の式として考える方法
3+６の後、4+7、5+8…8+11と続くと想定。前問の右辺を左辺と足して次の答えを出す
（A2）単独の式として考える方法
設問の ” 1+4 ” という表現は 1+(1×4) とう計算を表すとする裏公式を設定
1+4 → 1+(1×4) =5
2+4 → 2+(2×5) =12
： ：
8×11 → 8+(8×11) =96
+を使ってることに違和感覚えてる人多いけど、+に対する固定観念を捨てられるかっていうのもIQが高いかどうかの判断材料の一つなんだよな
※205
プラスやマイナスはいわば接続詞のようなもので
例えば右手に置く、と右手を置くではにとをの違いで全く意味が異なる。それと同様に固定概念云々ではなく、これに関しては言語として間違いになる
言いたいことはわかるがそれはそこで使うには適当言い方ではなく別の意味ととれて、この問題は問題が機能不全を起こしてるとみられてる
すぐ96にたどり着いたが
計算は掛け算だったわ
77＋8＋11=96より
8＋11×8=96のほうが正しいっしょ
じゃないと0＋3や－1＋2を入れたときに説明がつかなくない？
A+B=…
としたら
A+A×Bでもいける。答えは2つ目と同じになるけど。
40と96
法則があるからそれだとどちらも出る
1×4+1=5
2×5+2=12
3×6+3=21
8×11+8=89
俺はこれだった
1000人に一人ならIQは約146(146.3535)
IQ130なら約44人(43.95585)に一人
1個目の方が難しいやろ
2個目は＝の左側の数字はただの順番を示す記号だと思えばすぐに出てくるけど
1個目がひらめく奴の頭どうなってんだ
5年後の新しい回答。
V字で数字を追ったときの掛け算になっている。