詭弁、あら捜しなど、ネット上で良く見る書き込みはある法則に基づいていた。目からウロコの面白い10の法則・効果

この画像を大きなサイズで見る

　マーフィーの法則やピーターの法則くらいなら聞いたことがあるかもしれない。だが、世界には人生や人間などを理解するための知恵が凝縮された法則はたくさん存在する。

　ここでは目からウロコの面白い10の法則や効果ひも解いていこう。

1. スキットの法則

この画像を大きなサイズで見る

　他人の文法やスペルの誤りを指摘するコメントを残したくなる人は、スキットの法則を覚えておこう。

　つまり、「他人の投稿の誤りを指摘する投稿には少なくとも1つの誤りが含まれている」のだ。

　どこかカルマらしきものも感じるが、これについて投稿者の意図についてより寛大な見方もある。つまり、「投稿に間違いが含まれる確率は、それによって投稿者が感じる恥ずかしさに比例する」というのだ。

　この法則を指摘したのはスキットが最初ではない。1990年に提唱されたベルのユーズネットの第一法則が一番古いものだろうが、一番簡単に覚えられるのは1992年のマフリーの法則（Muphry’s Law）だろう。これはマーフィーの法則（Murphy’s Law）の誤記だ。

2. カニンガムの法則

　これはスキットの法則とも関連がある。カニンガムの法則によれば、「ネットで正しい答えを得る最善の方法は質問するのではなく、間違った答えを投稿すること」だ。

　ネットの住人は助けを求める声はすぐ無視するが、最初の投稿主よりも自分の方が賢いことをひけらかす衝動には耐えられないのだ。

　この法則はスティーブン・マクギーディが提唱し、法則の名前はWikiの発案者であるウォード・カニンガムから取った。スティーブンによると、ウィキペディアはこの法則の一番有名な例だという。

　カニンガムの法則はフランスのことわざ「precher le faux pour savoir le vrai」（偽りを説いて真実を知る）をインターネットで応用したものとされる。

3. ゴドウィンの法則

この画像を大きなサイズで見る

　ヨーロッパで人を評するうえで最悪のものは、ヒトラーに例えることだという。国によって例える人物や対象に違いがあるが、悪名が高かったり、嫌われる人物や組織であることは確かだ。

　マイク・ゴドウィンはネットにこうした傾向があることに気がつき、1990年に「ゴドウィンの法則」と呼ばれるようになった。

　この法則は、「オンラインでの議論が長引くと、ナチスやヒトラー（悪評のある人物や組織）との比較が行われる確率は1に近づく」と説く。

　実際には、自分にとって不利な状況を打破しようと悪人を引き合いに出しているだけで、有用な情報など何も持っていない。

4. シャーキーの法則

　クレイ・シャーキーの著書は大半がネットや新しいメディアをメインテーマとしているが、シャーキーの法則は世界にすら当てはまる。

　それが説くところは、「制度はそれが解決すべき問題を維持しようとする」だ。

　例えば、ある組織が手順を簡単にしようとしているとする。そのために委員会を設置したり、新しい管理レベルを作ったりする。が、こうして官僚的な層を追加するほどに、手順はますます複雑になっていく。

5. ピザの定理

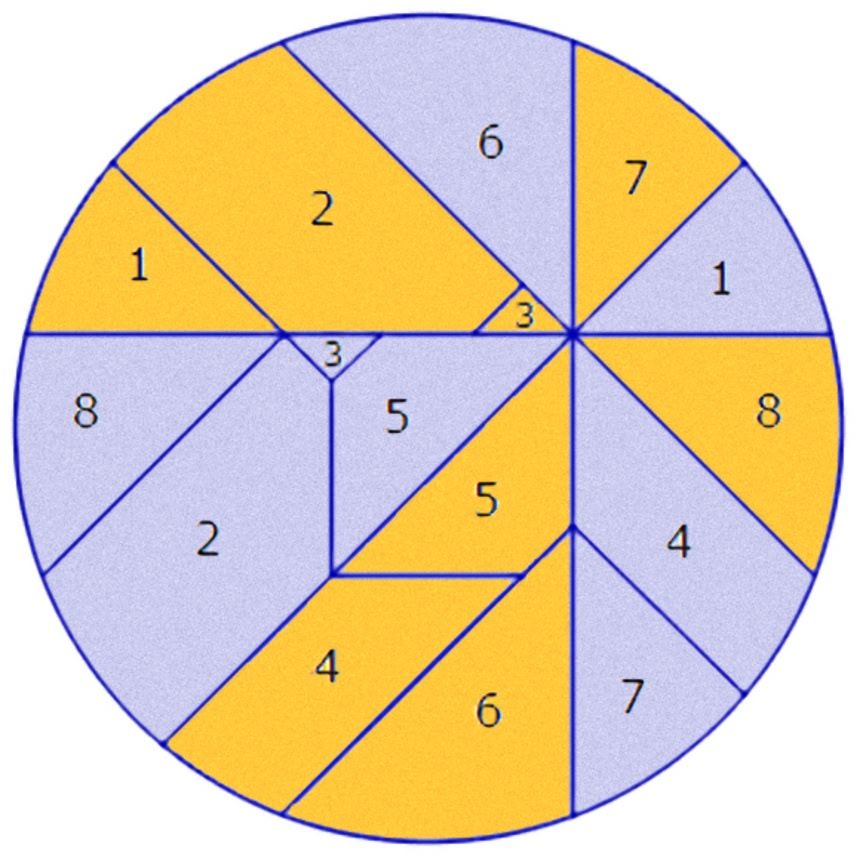
この画像を大きなサイズで見る

　ピザの定理は「ピザの任意の点をとり、そこから均等な枚数に切り分けられる」と説く。交互に並ぶスライスの面積の合計は等しくなる。

　ピザを分ける相手が自分ともう1人だけのときは便利だ。だが、もっと簡単なピザの定理もある。厚さ（a）と半径（z）を用いてピザの体積を計算するのだ。公式は次の通り：p i z z a（ピザ）

6. アーカムの剃刀

この画像を大きなサイズで見る

　オッカムの剃刀は、「問題を解く、あるいは結果を予測するために、1つ以上の説明があるのならば、一番シンプルなものがおそらくは正しい」と説く。

　その真逆の法則がアーカムの剃刀だ。これはフィクションの世界、特にコメディで当てはまる。

　すなわち、「ある出来事について複数の説明があるならば、一番ありえないものが真実だ」というものだ。コメディのエッセンスは奇想天外さなのだ。

7. ストライサンド効果

この画像を大きなサイズで見る

　何かを隠そうとしたら、逆効果になってしまうのがストライサンド効果だ。これは歌手のバーブラ・ストライサンドに由来する。

　彼女は2003年に上空から自宅の写真を撮られ、これをプライバシーの侵害であるとして、政府公認のカリフォルニア海岸記録計画を訴えた。

　訴訟前にこの写真について知る者はほとんどいなかったが（6回しか閲覧されていなかった）、今では誰もが知るところとなった。ちなみに彼女は裁判で負けている。

8. ベターリッジの見出しの法則

　ベターリッジの見出しの法則は、「疑問符で終わっている見出しの答えは『ノー』」と説く。答えが「イエス」ならば、見出しは単純に断定的になるのだ。

　見出しの疑問は次のいずれかを示唆する。1) 筆者には答えに確信を持つだけの証拠がない、2) 得られる情報をセンセーショナルにする、3) 筆者は読者の意見を率直に求めている。アカデミーの世界にはヒンチクリフの法則という同じ法則がある。

9. バター猫のパラドックス

　矛盾する2つの法則があるとき、それをパラドックスという。バター猫のパラドックスは次のようなものだ。

　バターを塗ったトーストを落とすと必ずバターを塗った面から落ちる。猫は必ず足で着地する。なら猫の背中にバター塗りのトーストをとりつけて落としたら、猫もトーストも地面には落ちないはずだ。

　この現象のポテンシャルエネルギーの利用も考えられる。だが、実証して見せた者はまだいない。

10. コーエンの法則

　ジェフ・コーエンの観察によれば、「承認待ちのグループがモデレーターを作るかどうかについていずれ大ゲンカをする確率は時間とともに1に近づく」。これをコーエンの法則という。

via:10 Rules, Laws, and Theorems You Should Know/ written & edited by hiroching

• #面白
• #雑学
• #あるある
• #ヒトラー
• #法則