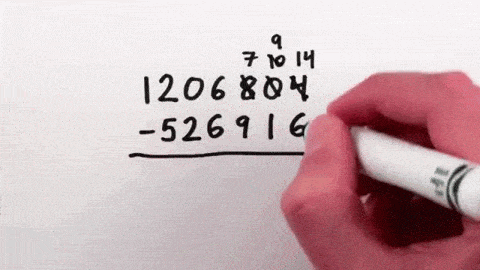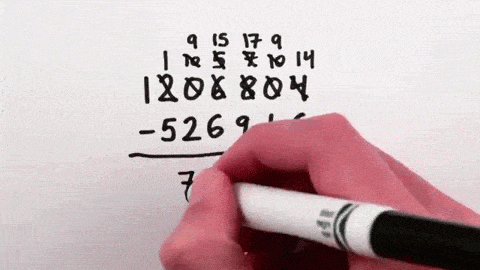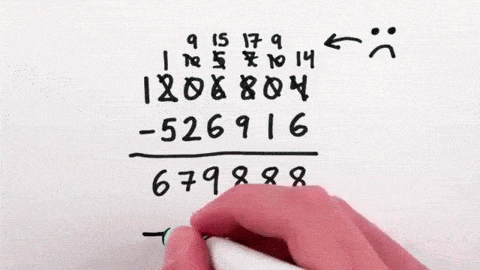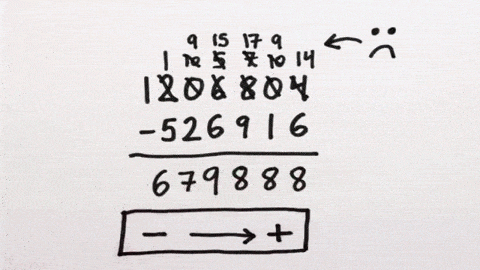この画像を大きなサイズで見るアメリカで暮らしたことがある経験がある人なら知っているだろう。アメリカではお釣りをもらう時、引き算ではなく足し算なのだ。例えば550円の品物を買ったとしよう。1000円を渡すとレジの人はお釣りを渡す時、550円を起点として、600円、700円、そして1000円と足しながら釣り銭を渡すのだ。
更に彼らは少数よりも分数で考える。25セントがクウォーター（4分の1）と呼ばれている点からもわかるだろう。
日本人ならなんてまだるっこしいことを！、と思うかもしれないが、アメリカ人は引き算が苦手なのである。確かに引き算のやっかいな点は、桁が長くなるほど、ややこしくなってくることだ。繰り下げも、桁が増えるほどめんどくさくなる。そんな人には、足し算で引き算の答を出せる方法をおすすめする。
その法則はこうだ。
１の桁以外の各桁の数字を9から引く。
１の桁は10から引く
それに大きい方の数値を足す
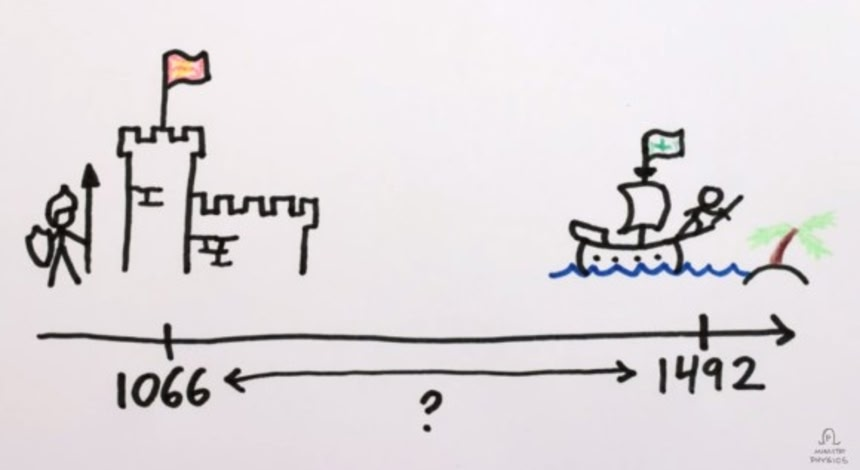
例えば、ノルマン人が英国を支配してから（1066年）、クリストファー・コロンブスがバハマ諸島発見し、キューバに上陸（1492年）までの期間を計算したい場合、まず、一の位を除いて、9からそれぞれの数字を引く。一の位は通常通り10から引く。
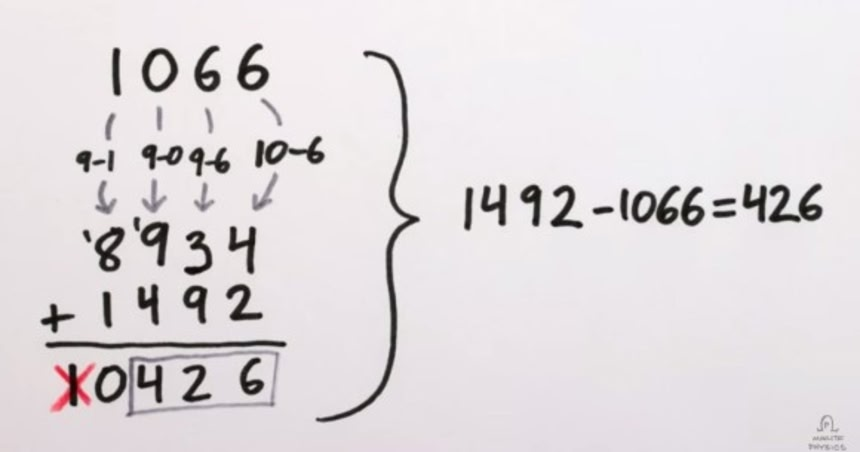
この画像を大きなサイズで見る1066の場合、左から9-1で8、9－0で9、9-6で3、10-6で4、それを並べると8934となる。そこに1492を足すと10426となる。そこから左の数字を消すと、0426という数字が導きだされる。この数字こそが1492-1066の答えとなる数字だ。
この画像を大きなサイズで見るっていうかまあ、日本人なら普通に1492-1066で計算しちゃえばいい話なのだが、そこはカルチャーの違いってことだ。
ちなみにこの足し算をつかった引き算は、正の整数ならどの数字でも適用することができる。
8-6=2、これは、8+(10-6)、8+4=12の左の位を除いた数、2となる。100-001は、100に、9-0、9-0、10-1、999を足した数1099の一番左の位を消した数、99となる。424242-333333は、424242に666667を足した数の1090909の一番左の位を消した数、90909となる。
この画像を大きなサイズで見る余談だが、この方式はコンピューターでも使われている。ただ、コンピューターの場合は、2の補数を用いた減算と呼ばれ、バイナリ（二進法）が用いられるため、もっとシンプルになっている。
めんどくさい！！と思ったとある日本人です。
引き算苦手でなくてよかった
あー、なるほど補数の計算か
10進数で補数計算ねんて考えもしなかった
意味が分からない
引き算でした方が早かった。。。
なにこれむずかしい
2の補数表現しか知らなかった
引くよりこっちのが楽なのか…それはそれで才能？
英語圏は10進数が直感で解りづらいらしい
言語的にtwelveで区切りが来る
ダース計算の世界なので
ハーフ、クォーターの考え方が得意なんだって
余計にわかりにくくなった
10進数でやる意味皆無
1と0しか無いからええんや
ごめん、全くわからない…
これはアメリカだけなのかね
※12
とても興味があるので、もう少し詳しくそのお話について教えて下さい！
足し算で引き算って9ー1とか引き算しとるやん
普通に引き算した方が早かった
※14
オレは普通にやるぞ。珠算の見取り算でも最後がマイナスになる時は、補数で表すみたいだよ。
※36
気にする理由が分からない。紙幣でも貨幣でも、金には違いがないじゃん。
おおー、これは面白い。使うことはないかもだけど。
アメリカではお釣りを渡す時･･･まで読んだ
だから俺は大人になってもさんすうが出来ないんだな
面白いね
でもこれ出来る人は引き算出来るよね…
2進数で補数を使って加算で減算する方法に衝撃を受けた事を思い出した。
その直後に加算のみで四則演算が可能と言った教授に更に衝撃を受けた。
掛け算は足し算の繰返しで、割り算は引き算の繰返しだと聞いて納得した。
まだ8ビットが主流の世界だったけれど、64ビットとか256ビットだと手書きで計算する場合に今なら確実に桁落ちさせる自信がありますね。
ビットコインを手動で導き出す教授もいるので不可能ではないけれど、当時から何で計算機を使っちゃ駄目なの？って思った。
この記事を読んで改めて計算機を使えば？と思う。
2進、8進、16進はその時以来殆ど使ってないけれど、時々Ｃｏｌｏｒ表現で16進表記を見掛ける以外はＰＧで予想外の計算結果の時に桁落ち溢れを疑う位かな。
これ数式にするとなんと面倒いかに面倒なことをしているかわかる。
1492－1066＝1492-1066 +10000－10000
＝1492+（10000-1066）－10000
＝1492+8934 -10000
＝10426 -10000
＝426
いろいろな方法を知っておくのは良いかもしれないね！
でも、めんどくさいよね！ね！
ぜんっぜん分かんない。
やばい？
余計わからん。普通に引き算したほうが１０倍早い
550円の物で1000円出されたら、550円にいくら足せば1000円になるか計算するわ。
先ず550円に50円足して600円。あと400円足せば千円になる。つまり450円足せば千円＝おつり450円ってすぐ解る。
小学校で習う上の桁から１かりてきて～が意味わからんかったから、当時自力で編み出した。
さっぱり分からん・・・
習慣の違いなのか、脳そのものの違いなのか。。。
microsoftもappleもgoogleもtwitterもfacebookもアメリカの企業
こういう考え方自体の違いが根本にあるのかもしれないね
普通に引き算した方が速い、というのも固定観念なのかもしれない
それに縛られるから柔軟な発想ができない
面白いなぁ
引き算すごく苦手だからか分からないけど、この方法めちゃくちゃ良い！
暗算ではなく筆算に限るけど
ヨーロッパでもわりとそうだよ
550円のもの買って1050円渡そうもんならわけ分からなくて怒られる
「足し算で引き算の答えを出す」はずなのにいきなり「１の桁以外の各桁の数字を9から引く」と言われて混乱した。
アホ丸出しの俺氏、むせび泣きそうになる。
アメリカだけでなく、ヨーロッパもそうだね。
昔フランスで、52Fの物を買うのに100F渡すと、53 54 55 56…と数えながら渡された。
何まどろこしい事やってるの？って思ったよ。
子供の頃に教えられた計算方法が染みついてるから、同じ計算式を習った者同士だと、発想が似通って来るのかな？
色んなやり方を子供に教えて、自分に馴染む計算式をチョイス出来るようにしたら良いよね。
※35
これは自分も経験した。あいつらは財布が小銭でじゃらつくのを気にしないらしい。
※30
それまさにアメリカ人と一緒の考え方やわ
※38
いや、小銭がじゃらつくと、財布が膨れるし、重くなるし、違いはあるだろ・・・。
※38
小銭で財布が膨らんでると、みっともないだろ 財布も痛む
それすら気にしないなら…うん 何も言うことはないな
※30
私はおつりのコイン数が最少になるように計算しますね。 550 円で、手持ちにコインが 550 円分ない時に、千円札に 50 円をつけられるかを捜索します。 だから、おつりがいくらかであるかはあまり考えたことなくて、引き算もほとんどしてないなぁ
※35
アメリカでは、おつりが切りの良い金額なので感動された事あるぞ。
みんなのコメントでようやく分かった気がする
どうりでクレジットカードが普及するわけだ
日本で言うところの万単位とキロ単位みたいなもんなのかな
伝統や慣れ親しんだ手法の方が効率が悪く見えても早く物事を解決できる的な
天才の思考してる人にとって凡人はこういう思考をしてる風に見えるんだろうな
そろばんやっててよかった
こういうので苦労した覚えがない
俺はてっきり、1492-1066=1492-1100+34=392+34ってやるんだなと思ったら・・・
頭いいなアメリカ人はこんな複雑な計算を編み出すとは。
2,3桁の補数を求めるのも欧米人はしんどいのか。
一個人の考えに対して、国を持ってくるの滑稽だからやめーや
引き算より割り算が苦手なんだが…
足し算の繰り上がりがあるから結局面倒
アメリカ人は逆に頭が良すぎるんじゃないのか？(理解不能)
引き算の暗算が呆れるほど苦手で、
筆算してる様子を思い浮かべて計算して、その途中で脳内に書き込んだ数字を忘れて……というひどい有様だったけど、試しに足し算で計算したら空想の筆算も使わずかなりラクにできた！
カラパイアには今まで何度も助けられています
ありがとう
国によっちゃ釣りの小銭を気にするのはみみっちい奴だったりするのも
引き算しない習慣からなのかね
多分人間の本能として、位取り引き算がすごく難しい概念で、身につけるためには幼い時から徹底的に反復学習する必要があるけど、この方法のだと本能的に理解しやすいんじゃないかな
言語の体系からすると、日本語(漢語)は十進法にかなり最適化されてるけど、コメント欄にも何人か引き算が苦手な人がいるみたいだしね
おそらく母語の数体系とはそんなに関係ない話なんじゃないかな
これは補数の概念を説明するとき都合が良い。 ２進数の場合、補数に変換する場合、各桁のビットを反転して＋１すると教えられる。
機械的に変換する方法は容易く覚えられるが、意味を理解しているかどうか怪しいものだ。
１０進数で補数を表せば最上位桁より１を引けば各桁はすべて９になる。 足して９になる数が補数で最後に１を足したのは最初に１を
引いたから。 すべての桁が９なので引き算をする場合桁借りが無い。 ２進数の場合は１を引くと各桁が１になる。 引き算だから
ビット反転、最後に１を足す。
補数変換は基本的には引き算。 １０進数を引き合いに出して補数を説明した方がわかりやすい。
この記事の説明がわかりづらいだけ。
レジ打ちバイトやった事ある人や会計士なら意識しなくとも自然とこういう計算法をしてることが多い。
「大きい方の数値から小さい方の数値を引く」というのが日本人の一般的な考え方。
一方これは「小さい方の数値にいくら足したら大きい方の数値になるか」という考え方。
例えばアマゾンで買いたいものがたくさんある時(クレジット払い)、今月の預金残高の50,000円から欲しい物の値段を引いていくよりも、0円の状態からとりありずカートに入れるだけ入れて金額を超過した分だけを引いていく。
これと同じ考え方。
僕も日本人ゆえめんどくさい！と思う。
しかしながら、足し算で引き算をする考え方は興味深い。
これがコンピュータ演算の基礎になり、二進数、補数(1の補数、2の補数)へと洗練されていくのだからさらに感慨深い…
フランスは20進法でもっと複雑やからな。なんでそうなんねん。