image credit: youtube
数学の中でも図形が一番苦手！なんて人も、図形が動いてくれたら親しみやすいかもしれない。これは海外掲示板で取り上げられた幾何学系GIFアニメで、多角形の外角の和が360度になる例を示したもの。
4種の多角形がだんだん小さくなって、その外角が円に！これなら直感的にわかりやすいと評判を呼んだのだ。
広告
Exterior angles, by magic pi - math animations
4つの多角形の外角が円に
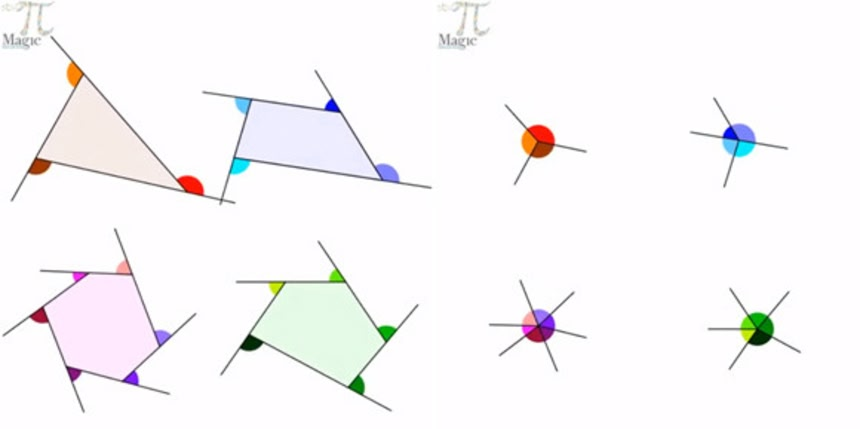
カラフルな外角を示す三角形から六角形の4つの図形
image credit: youtube
その図形が次第に小さくなり区別がつきにくくなってもまだ縮んでいく
image credit: youtube
するとそれぞれの外角が組み合わさって円に！
image credit: youtube
多角形の外角の和は360度
さて、数学の中でも幾何学なんて記憶のかなた…な人は私だけではないと思うが、以下の動画を参考にざざっとまとめてみよう。無料学習サイトeboardの動画より
なぜ外角の和は360°になるのか？
n角形の外角の和は、n角形の内角と外角の和から、n角形の内角の和を引けば求められる。
外角は、ある頂点をなす角の2辺のうち、1辺を延長した時の内角の補角を指す。つまり1つの内角と外角の和は180度なので
n角形の内角と外角の和は 180xnになる。
一方、n角形の内角の和は 180x(n-2)で求められる。これは多角形に含まれる (n-2) 個の三角形を表している。ちなみに、三角形の内角の和は180度だ。
そこで、n角形の外角の和は 180xn-180x(n-2) =360
よって360度となるのだが、冒頭のGIFは4種の多角形でそれを示している。
ぱっと見でわかる！証明じゃない！という声も
このGIFをredditユーザーのTransPlanetInjectionが「多角形の和360度を視覚的に証明」というタイトルで投下すると、さまざまな反響が巻き起こった。この件に関する海外の反応は...
・数学を教えてるんだけど、ちょうど明日これをやる予定だったから助かった！投稿に感謝。
・概念を視覚化してわかりやすくする非常に単純なやり方だ。
・角に線を引いて180度を添えてあるおかげでとても分かりやすい。
・数学の先生がこれを見て教室で使ってくれたらいいなぁ。
・数学の授業でこういうGIFをたくさん使っているわ。ただ、これを見た子どもたちは定理で使う言葉を覚えずに映像だけ覚えちゃうみたい。
・証明じゃなく視覚的な参考例の一つ。
・合わせて360度になるのは伝わる。でも4種類の多角形しか使ってないところが引っ掛かるかな。
・おお！やっと今、GIFの意味わかったわ。
・直感的な理解にとても役に立ったよ。ありがとう！
・私もこれ授業で使わせてもらおう！
イスラエルの数学教室の投稿アニメ
反響を呼んだGIFはイスラエルの数学教室、Magic PIの教師たちが作ったものだ。彼らは数学の楽しさを伝えるために一目でわかるアニメーションを多数シェアしている。Magic PI - math animationsのフェイスブックより
多角形の内角の和=360度の例
三角形の内角の和=180度の例
ピタゴラスの木(フラクタル図形)
確かにこうして動いてくれると概念が伝わりやすいかも。
見るだけで数学に親近感が持てそうなアニメの数々。Magic PIのその他の作品はフェイスブックやインスタグラムをチェックだ。
References:reddit / youtube / youtube / facebookなど /written by D/ edited by parumo
あわせて読みたい
教会にある幾何学模様「フラワー・オブ・ライフ」(生命の花)の意味は？
不思議な錯視シリーズ。素早く瞬きをしながら見ることて、見えないものが見えてきた！
植物のフラクタル感にうっかり惑わされてみる
計算しようとすると頭がパニックになる。できることなら数字を避けたい。「数学恐怖症」に関する事実とその克服方法
生後6か月でその子の数学的能力が明らかに。その見分け方とは？伸ばし方とは？（米研究）
0
3485
1
11
コメント
1. 匿名処理班
わかったような気にはなる
2. 匿名処理班
この動画見るまでこんな発想浮かばなかった
IQ高く生まれたかった
3. 匿名処理班
n角形の外角の和は、n角形の内角と外角の和から、n角形の内角の和を引けば求められる。
外角は、ある頂点をなす角の2辺のうち、1辺を延長した時の内角の補角を指す。つまり1つの内角と外角の和は180度なので
n角形の内角と外角の和は 180xnになる。
一方、n角形の内角の和は 180x(n-2)で求められる。これは多角形に含まれる (n-2) 個の三角形を表している。ちなみに、三角形の内角の和は180度だ。
そこで、n角形の外角の和は 180xn-180x(n-2) =360
こういう文見るとあ、もういいやってなる
4. 匿名処理班
視覚的にはわかりやすいけど
ヒトの脳は正常な状態でも錯覚がおきる
ネタとしては良いけど教育現場で使うのはどうかと思う
5. 匿名処理班
大した事考えなくても
図形を一回転させれば元の位置に戻ってくるやん
だから360度ってだけで何も難しくないやん
6. 匿名処理班
これを数式で証明できないと意味がないし、応用も発展も無い
知ったつもりは発展を阻害するから
興味を引いたその後の導きが重要
生徒も教師もガンバレ〜、ファイトだ
7. 匿名処理班
オレが思ってる『多角形の外角』ではなかった。ありがとうございました。
8. 匿名処理班
導入として非常に良い視覚効果だと思う。
幾何はまだ視覚的に捉えやすいとはいえ、こういった工夫を凝らして教える先生方は大変ですわ。
9. 匿名処理班
イメージがハッキリすると納得度が高くなるので
何事も納得しないと頭に入ってこない人にとってはかなり良いものだと思う
10. 匿名処理班
凹多角形の場合にも適応できるね
11. 匿名処理班
円がボコボコしただけなんだから当然360度だと子供の頃理解してた
12. 匿名処理班
この動画を作った人は、プラトンのアカデメイアの門をくぐれるな。
13. 匿名処理班
※6
人の数だけ取っ掛かりがあって良い。
最終的に真理にたどり着けば良いわけで、
その導入にケチを付けるのはどうかと思う。
14. 通りすがり
>>10
引き算しないと360度越えちゃう
15. 匿名処理班
この変な形を計算させられまくる理由は
いつまでたっても教えてくれないんだよね。
「解けたら将来月収何十万円見込めるから
解けるようになりなさい」とか
教科書に生々しく書いててほしかった。
16. 匿名処理班
学校でこれ見たかったなー！
目で見て分かりやすいのは嬉しいよ。
17. 匿名処理班
※15
解けたら将来月収何十万円を稼げるアイディアの種になるかもしれないから
解けるようになりなさい。
18. 匿名処理班
タイトルにGIFアニメってあるのに、貼ってあるのはGIFじゃなくてYouTube動画なのはなんでなん…？
19. 匿名処理班
目の錯覚現象を紹介する系の面白動画と、雰囲気がものすごく似てる。
20. 匿名処理班
えっ、コレ普通に学校で視覚的にも教えられなかった？
21. 匿名処理班
※20
図形をバラして角を合わせてほら360度だねってとこまでの説明ならよくあるけど、
この動画はどんな角度の何角形であっても360度になる理由まで理解できるってのがミソ
22.
23. 匿名処理班
僅かばかりとは言え数学を齧った身からすると、※6の評価が低いのはすごく悲しい気がするなあ……
数学は目で見れば一発のことを小難しく屁理屈こねてると思われてるのかもしれないが
「目で見ればわかる」が「目で見ないの分からない・納得しない」になってしまうと「目に見えないものは分からない」に陥る危険性がものすごくある
逆に、一部の数学者には四次元や五次元という見えるはずのない世界が「見える」というのは割とよく聞く話
具体例をもとにしながらも、なるべく抽象化することで、逆に応用に際しては具体に依存することなく何にでも適用できるようになる、というのが数学の真の力・真の魅力だとおもうのだけれど、そこにたどり着くまでの道のりが茨の道すぎるのかなあ
24. 匿名処理班
※23
「数学的思考が出来ない人でも分かる方法」って話題なんだから
冷や水ぶっ掛けなくてもいいじゃん！ ってなっちゃったんですよ、多分