この画像を大きなサイズで見るAdvertisement
面白い錯視的動画が公開されていた。「クレージー・サークル・イリュージョン」と題されたその映像は、白い8つの点が円形を描き回転しているように見えるのだが、実際にはすべてが直線に動いているのだという。
これも錯視の一種なのだそうだが、確かに最初の映像では円形に並んだドットが赤色の円を回転しているように見えるよね。
でも分解してみてみると、それぞれが直線をいったりきたりしている
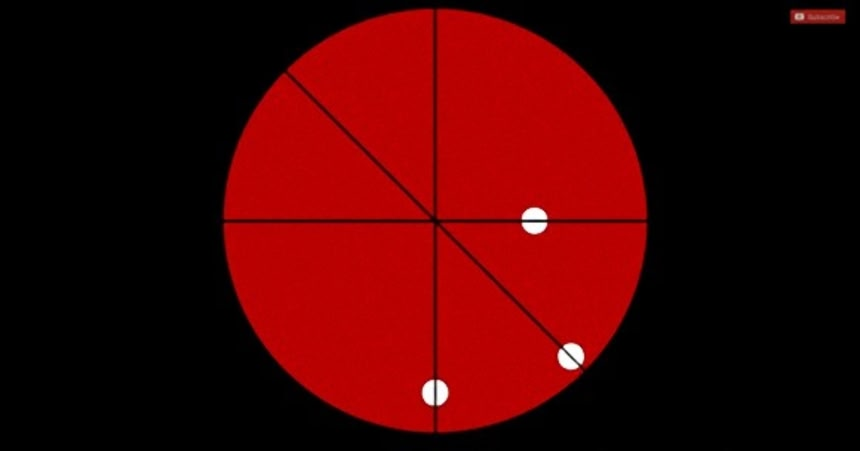この画像を大きなサイズで見る
この画像を大きなサイズで見る
この画像を大きなサイズで見る
この画像を大きなサイズで見る
この画像を大きなサイズで見るこれもいわゆる脳が騙されている状態なわけなのだろうか？錯視って面白奥が深いね。
📌 広告の下にスタッフ厳選｢あわせて読みたい｣を掲載中
ロータリーエンジンみたい。
ん？あぁーなるほどー
不思議だねぇ面白いわー
これは結構面白いけど、錯視の範疇じゃないと思います。
おもしろい
なんかこの動きを使って新型のエンジンとか作れないかなとか思った
直線運動で回転するように見せてるんだろ？
ン？錯覚？内サイクロイドで半径0.5なら直線を書くとかやったような
※6
マツダのロータリーエンジンが似てる気がするな。
中のロータがおにぎりみたいな三角だけど。
つまり、錯視を使えば直線の動きだけで回転を表現できるってことか。
加速度を調整してるじゃねぇか
サンプリング定理的な話？
これ周期合わせてるだけだから錯覚とはまた違うと思う。
錯覚とは実際とは異なる知覚を得てしまう現象のことらしいので
これは異なってないだから錯覚ではないと思う。
動いてないのに動いて見える。白黒なのに緑が見える。同じ色なのに別の色に見える。
こういうのが錯覚なんだと思う。
タイミング合わせてるだけじゃね？
これって外側の円と白い玉が描く内側の円の半径(直径)の比率がたまたま1:2っていう単純な(ある種特殊な)比率だから、
内側の円の白い玉の運動に着目したら違う直線上でそれぞれ位相のずれた振幅の同じ単振動してるって指摘してるだけでしょ？
別にそれは内側の円が回転していないということを示してるわけでもなんでもないと思うんだけど
白点が回転する様に描かれているのは事実なので、錯視、と言われると違和感がある。
面白いのはその描画アルゴリズムだと思う。
単振動ってこういう扱い方もできるんだな。
物理か数学の試験に出てきそうな。。。
錯視じゃねぇ！数学的に正しいわ。
これは白を繋いだ中サイズの丸を考えると実際に大円の内側にそって噛み合わさるように”運動”してんの。
んで、中サイズの円の各点を考えてやると実は直線上を動いてるワケ。
あと回転っていうけどさ、回転ってその場でぐるぐる回る動きのことをいうわけ。白は塗りつぶされてるんだから回転してるかどうかなんてわかんないわけよ。
回転してるのは白をなぞった中サイズの円。もちろん回転とは別に移動もしてる。
実に面白い
サインカーブは円運動から導かれているから
当たり前と言える。
フランスの初期の航空機エンジンの
ル・ローンエンジンに似た動きだなと思った
クランクが回るんじゃなくシリンダーブロックが回ってるやつ
星型エンジン
普通に星形エンジン。ゼロ戦もこれ。
やっぱみんなエンジンっぽいって思うんだな
日本語の概念の「錯視」とは違うかもしれないが、タイトルがイリュージョンだとそういう訳になっちゃうわけで、いちいち重箱の隅つついてないで、楽しめばいいんでない？こういうのって楽しむものでしょ？
円の外周上の点の軌跡がたまたま線分になる例なだけ。
内接する円が回転しているように見えるのは確かに視覚の補完作用によるものだけど
「8個のドットからなる一つのリング」と取るか、1個1個を独立したドットと取るかで
違ってくるんじゃないかと思う。
前者なら円周に沿って転がっているリングそのものはその中心を軸に回転していて、
この場合赤い円の円周に接してるドットの接点と正反対の一にあるドットの中心の
距離が赤い円の半径に等しいのでそのリングのドットの軌跡が単に円の中心を通る
線分上を往復しているに過ぎない。
おーもしれー
理屈こねてるやつは面白くないからとっととクソして寝てろ
物理専攻してる俺から言わせてもらえば円運動も調和振動も同じもんだわ。
三角関数学んだことがある人なら等価ってことがわかる。錯覚ではない。
星型エンジンだな
直線運動を回転させてるように見せてるわけではない。
赤円上で赤円の半分の直径の円のサイクロイド曲線を再現するとこうなるだけ。
なんで点同士が衝突しないの？
最後の方の映像、玉6個目ですでに曲線を移動しているように見えた。俺の脳、馬鹿すぐる。
白点に違う色付けて
もう一度みてみたい
難しいことは分からないけど流れてる音楽が好きというのが分かった
円周上の点の動きが直線になるのは当たり前じゃない？
※33
カリカリし過ぎ
気にしない
Wikipedia 「歯車」より 歯数の組み合わせは自由であるが、大きな力を伝達するときや、滑らかさを必要とするときは、いつも同じ歯同士が当たると、微小な傷が大きくなったり、特定の箇所で音が発生するため、歯数が互いに素になるように設計される場合がある。
つまり普通はこうならないように設計する
回転した時と全く同じ動きなんだから当然といえば当然。
おおー
面白かった
ポンデリングを円の中で回したら同じことが出来そうな気がする
音楽が良いな
集団運動でこの動きやったら面白そうだね。
歩く速度の調節が難しいだろうけど。
ていうか回転してるやんか
コレジャナイ感
スーパードンキーコングみたいなBGMにばっか集中してしまった
×回転してるように見えるけど点が順番に真っ直ぐ移動してるだけ
○点を図のように真っ直ぐ移動させると回転しているようにみえる
錯覚とは違う
そう見えるように作っている訳だし
同じ長さなのに違って見えるとか、止まっているのに動いて見えるようなのを錯覚というんだと思う
使われてる曲はbrusspupのmonolithだね
そもそも錯覚していないというねｗ
どちらにも見える状態ってだけで、無意識下で一方の状態のみが見えるようになるわけじゃない。
振り子運動がたてに見たらS字に見えるとか、そういうレベルの話じゃないのコレ
錯覚じゃないと思う
私には円の中の小玉で構成された円形が回ってるようにしか見えないんだけど みんなの意見からすると負け！って感じみたいね。小玉1個だったら直線的に見えるけど2個からもう回ってるようにしか見えないよ。
私が知ってるサイクロイドって円周に点おいてその円を直線上を転がしたときの点の軌跡しか知らなかった。こんなのもあるんだね。
円Aの中を内周する円Bの外形線を点にしたらそれぞれが円A内で直線往復運動をしてるって話でしょー
錯視とは違う気が
これは錯視だよ、無意識に見ると、同じ球の動きを追っているつもりでも
いつのまにか別の球、また次の球を追ってしまう
子供のころ、スピログラフの定規を持ってたの思い出した