全ての人や物事は6ステップ以内で繋がっている。「六次の隔たり」に大きく貢献したケヴィン・ベーコンのベーコン指数

この画像を大きなサイズで見る

　全ての人や物は6ステップ以内ですべてがつながっている。「六次の隔たり」、英語では「Six Degrees（シックス・ディグリーズ）」と名付けられたこの仮説は、スタンレー・ミルグラムの実験を裏づけとして広まったものだが、地球上の70億人全員が案外近い関係にあるというこの仮説は、多くの科学者を引きつけてきた。

　すなわち、世界に暮らすある人とある人は、友達や知人を6人も介せば間接的に知り合いになるのだ。この名称はジョン・グエアの戯曲に因んだもので、1991年には『私に近い6人の他人』というウィル・スミス主演の映画にもなっている。

　そして唐突だがここでアメリカの俳優、ケヴィン・ベーコンがでてくる。彼は無自覚ながらこの仮説の検証に大きく貢献したといたのだ。

有名俳優が学生と共に、「六次の隔たり」ゲームを考案

　アメリカの学生グループが”ケヴィン・ベーコンとの六次の隔たり”というゲームを考案した。ケヴィン・ベーコンは様々なジャンルの作品に出演していることで有名な俳優である。

　ゲームでは適当にハリウッド・スターの名前を挙げ、その俳優とケヴィン・ベーコンと共演したことのある俳優とのつながりから、ベーコン本人との近さである”ケヴィン・ベーコン数”を割り出す（本人と共演したことがあればベーコン数1、ベーコン数1の俳優と共演したことがあればベーコン数2という具合）。

　この遊びはネットなどでも大流行りした。その結果ハリウッドに限らず、ほとんどの俳優はベーコン数3以内に収まることが判明した。

この画像を大きなサイズで見る

六次の隔たり仮説を検証

　BBCでは六次の隔たり仮説を検証するために、1960年代に行われたある有名な実験を再現してみた。

　実験では世界中から無作為に選び出した40人の被験者たちに小包を渡し、自分のごく親しい人に郵送することで、どうにかボストンに住むマーク・ヴィダルという科学者に小包が届くよう手配してほしいと依頼している。

　その結果、小包3つが本人の許へ届き、そこに介在した人物の平均は6人であった。届かなかった残りの37個については、受け取った人に関心がなかったことが原因で途中で止まったものと推測されている。

　小包の1つはケニアの田舎にあるニャムワレ村に住むニャロカという女性から始まった。彼女はナイロビにいる叔母のマーガレットに小包を送った。

　次にマーガレットは、以前ナイロビに住んでいたニューヨーク州の友達に郵送し、その人物はボストン在住の友人に送った。結局、ヴィダル本人には7人目として無事小包が届いている。

　他の2つの小包が同じように6人のつながりで届いていることからも、完璧ではないにしても六次の隔たり仮説は正しいことが証明されている。

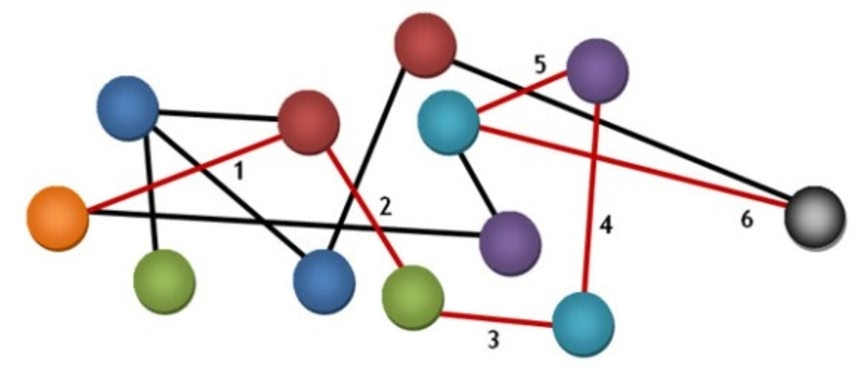この画像を大きなサイズで見る

　こうしたつながりを検証した実験は他にも多くあり、例えばマイクロソフト社は1億8,000万人が行った300億件のインスタントメッセンジャーの会話ネットワークを検証している。この研究からは、ある人とある人の間には平均6.6次の隔たりがあることが判明した。

科学分野に大きな影響を与えた六次の隔たり

　六次の隔たり理論は、他の科学分野にも大きな影響を与えた。

　数学者スティーブン・ストロガッツと当時博士課程の学生だったダンカン・ワッツはコオロギの鳴き声が同期する原因を調査した。

　ワッツはこの同期現象を解く鍵は六次の隔たりにあると考えていたが、これがネットワーク理論という新たなる研究分野を拓くことになるとは夢にも思わなかっただろう。

　この現象がコオロギの同期にも応用できるなら、伝染病の拡散や市場のダイナミクスについてはどうなのであろうか？

　この問いを念頭に、2人はケヴィン・ベーコンとの六次の隔たりで得られたオンラインのデータを用いて、そこから数学的な基礎を見い出せないか検討した。

　こうして導き出された目に見えないつながりを表す公式が広大な世界の小ささを、世界が”スモール・ワールド”であることを明らかにした。

　新しく登場したネットワーク理論は、ワールド・ワイド・ウェブ、都市の成長、世界的な移動経路、人々の性的関係、富の配分、細胞のタンパク質分子など、ありとあらゆるネットワークに応用された。

この画像を大きなサイズで見る

六次の隔たりで豚インフルエンザの拡散を予測

　米インディアナ大学のアレッサンドロ・ヴェスピニャーニ博士は、これを豚インフルエンザの感染予測に応用した。

　その予測の鍵となるのが、彼が流動性ネットワークと呼ぶ、人がある場所からある場所へと移動するその有り様だ。

　これには飛行機などによる長距離の移動も、短距離の通勤も、職場や自宅などの小さな空間での移動も含まれている。こうした経路を特定することで、次の感染地やその時期を予測することができる。

　前述した小包実験の”目標”であったマーク・ヴィダルは、病気の出所を発見するためにプロテインの相互作用を調査し、史上初となるいわばヒト細胞の道路地図を作成している。

　ネットワーク理論の重要性を過度に強調することに懐疑的な学者も存在するが、今ではすでに確立された理論となっている。これらの始まりにはケヴィン・ベーコンがいたのだ。

　君が死ぬまでに一度は会いたいと思っている有名人も、6人を間に介入させることでなんとか連絡をつけることができるかもしれないぞ。

追記：2015年12月の記事を再送してお届けします。

References: Knowledgenuts

• #雑学
• #豆知識
• #スモールワールド