この画像を大きなサイズで見る令和に突入した今日この頃、自分これで元号3つ目、三時代生きたんかぁ…と感慨にひたる昭和の人もいる中、ネット界では次世代を担う子どもの学習動画が反響を呼んでいる。
最近アメリカの小学生は新たな計算方法を学んでいるという。それは2桁のかけ算なのだが、旧世代が習った方法とはけっこう異なるものだった。
新しい方法と古い方法、2つの方法で同じかけ算を同時に解いていく動画が公開されていたのだが、これについて様々な反響が出ている。
新しい数学 VS 古い数学
この動画はユーチューバーのByler Tookstが「新しい数学 VS 古い数学」というタイトルで投稿したものだ。
映像がブレているため見づらいかもしれないが、左は最近のアメリカの小学生が習う、新しい2桁のかけ算のやり方で、右は以前のやり方だそうだ。
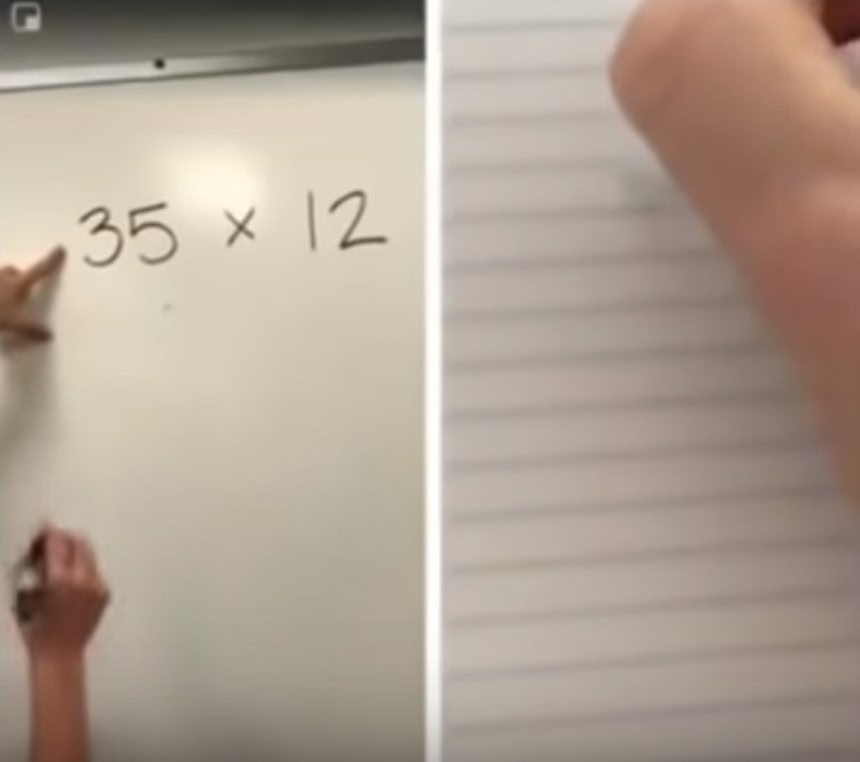この画像を大きなサイズで見る左：35×12を書いて説明スタート！ 右：ペンを持って計算スタート！
この画像を大きなサイズで見る左：35を30+5、12を10+2に分ける
右：従来のやり方でかけ算終了。答えは420とでた
この画像を大きなサイズで見る左：分けた数字と計算用のマスを準備中
右：終わったからコーヒーいれよっと
この画像を大きなサイズで見る左：左と上の各数字が交差するマスに掛け算の結果を書き入れる
右：コーヒーができるまで愛犬たちと戯れる
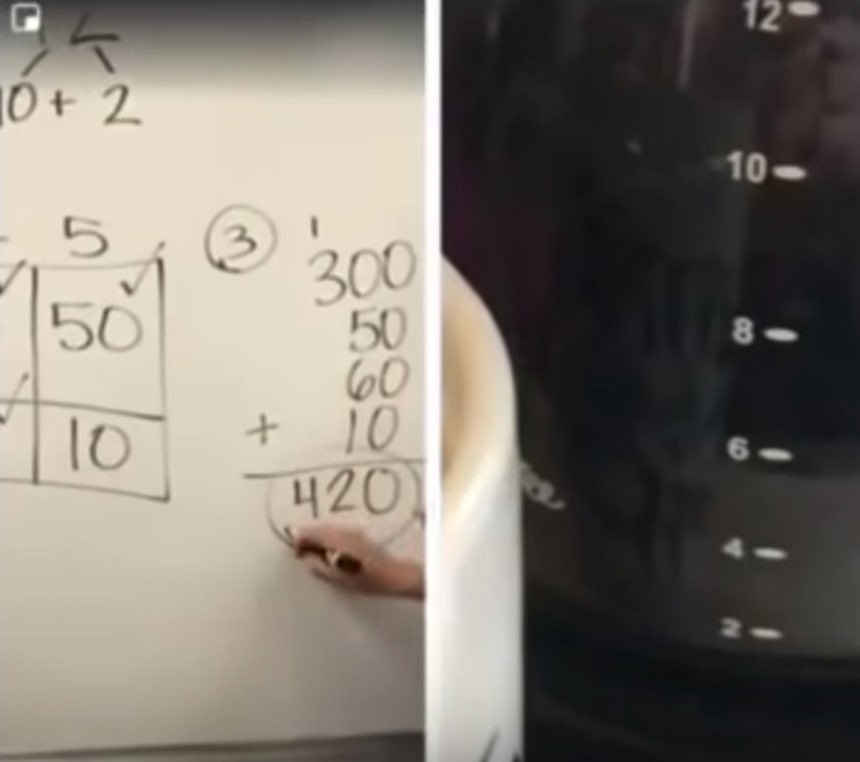この画像を大きなサイズで見る左：各マスの数字を書き出して足す。300+50+60+10で答えは420
右：できたてのコーヒーもカップに注ぎ終わってる
よくわかる新しい方法と暗記中心の昔の方法？
さて、右のほうが断然早く終わる！って感じの映像だが、ネットユーザーからはこんなコメントが上がっていた。
この動画に関する海外の反応は…
・35 x 10 = 350 35 x 2 = 70 350 + 70 = 420
・ていうか、暗算する人って脳内でどうやってんだ？こういうひっ算は紙とかあるのが前提だよな？
・左側の35を30と5に分ける方法は35の倍数がわからない人のためのやり方で、説明しながら計算してる。
・右のは説明も無しでいきなり計算してる。この動画は完全に論理的なものを嘲笑してるみたいだ。どちらの方法も間違ってないと思うけど、やり方の説明がなければ役に立たないよ。
・ 「なぜそうするか」って説明は本当に重要だよね。私も子どもの宿題をみるようになって実感してる。私の世代は基礎を理解しない暗記がメインだったけど、今の子どもたちは基本的な知識を教わっているもの。
・昔の習った家庭教師が「アメリカの数学は長さ1マイルで深さ1インチ」と言ってた。小学校で基礎を習ってるうちは時間がかかるから長く思える。でも概念さえ理解すれば中学で簡単になるって。逆に、なんでも暗記でやってきた多くの子ども（自分も含む）たちはつまずくようになるらしい。
・こういうの大事だと思う。うちの子は小学2年生だけどなぜそうするのかがわかれば私よりずっと難しい問題を解きそう。今更だけど左側みたいな教え方をしてもらいたかったなあ。
・自分はいつも数学で「どうして？」って疑問を持ってたから苦労したよ。概念がわからないと身につかないし暗記するほうが大変だもの。
・これって本当に「新しい数学」なのか？ただ長ったらしく説明してるだけじゃね？
・「教える数学」と「やり慣れている数学」の違いみたい。
・単純に教えてるというより、この計算方法の初歩の授業だろう。小学校4年生以上かもしれない。
というわけで、海外ユーザーの間では左の方法に感銘を受ける人が多かったようだ。
ちなみに昭和世代の私の場合は右のほうが断然なじみがある。もはやうろ覚えなんだけど、最初に九九を覚えてから二桁の掛け算をやったような。
今時の日本の小学校はどうなんだろう。実は左がメジャーになってたりするのかな？そのへん詳しい人よろしくだよ。
References:reddit / youtubeなど /written by D/ edited by parumo
なるほどね、本質的にはどっちも同じだけど左のほうが面積の理解とも直観的に結びつくからメリットはありそうだ。
左みたいに掛け算程度でわざわざ長ったらしくバラしてやる必要あるか…？
※2
理屈だけなら右を繰り返してればいつか気づくし気づかなくても方法論的に優れてるんだよね
左を見て納得できる人はたぶん地力に優れてるんだと思う
自分は左をぱっとみても理解できないから最初に右を教えてもらったほうが効率いい
左は因数分解へのとっかかりもかねてるんでしょ
初めての人に教えるのと、既に知っている人が解く時間を比べるのは公平じゃないな
新しいやり方の方が時間はかかりそうだけど、因数分解とかはこっちで習ってた方が理解しやすそう
小学校も面倒くさいよ
文章問題の式で例えば
3×2=6 2×3=6
で答えは一緒なのに順番が違うと×とか
どっちでもいーじゃんと思うけど
かける数とかけられる数は違うんだとさ
>>5
掛け算の順序問題というwikiの項目があるよ。
まあ、専門家の間でも意見が別れているようだな。
>>5
文章題は国語でもあるんだよ。
りんご３個入りの箱が５個
りんご５個入りの箱が３個
個数は同じだけど意味は違う。
意味を正しく理解してることを数式で説明するのが文章題だから、説明になってない式を書くと減点されてしまう
パッと見た時に350+70で暗算してたから思考的には新しい方がいいのかもしれないね
コーヒー淹れ始めるの笑うわ
確かに冗長だけど初めてやる分には新しいやつのほうがわかりやすそう
今は、電卓でもなく
Googleで検索か、スマートスピーカーに聞いてるのでは？
たすきがけだよね
20年位前に小学生相手の家庭教師をしたとき、鶴亀算等々の方法の代わりに
面積図というものを使用する方法を教わったことを思い出した
この問題に限れば35×12＝35×2×6＝70×6＝420の方が早いかな
暗算する人の中のイメージに合った方法を都度選ぶのがいいと思う
右でパパッとやる方が一件効率よく見えるけど、今後の数学の履修を考えると左のやり方が理に適ってるのかな。
>>11
数学が得意な子どもたちは右を習いながら頭の中では左の方法やら色々やるみたいだよね。
筆算は桁数がそれなりにあっても便利に利用できるけど、件のやり方は３桁以上の掛け算になると途端に実用的じゃなくなるし筆算よりも早いかって言われると微妙な所なのがね…
みんな言っているが、理解させる、という点で左の新式は優れている。
こういうのを揶揄すべきではないよ。
左の考え方なら(35+35)+6とかの方が早くね？
桁が増えたらどうなるんだ？
>>15
3ケタ同士なら、3行3列の9マスになるよ。
インドとかでも斜めに線か何か引いて同じような事してたと思う。
～違いがわかる男になりたい～
170
350
420
(ﾟДﾟ≡ﾟдﾟ)ｴｯ!?
※17
７と５を足して繰り上がった１を記入しているだけだよ
>>17
どうしても35×2=170が解らなくて何度も考えたw
なんかやたら筆算を排斥する動きは日本でもあるよ
さくらんぼ算とか取り敢えず各桁バラして計算する
各々の計算は簡単になるが足し算が増えるから間違えやすいんだよね
39×12とかだと（40-1）×（10+2）とかもやるのかな？
暗算だと12×(40-1)が早いかも
日本ではエアー珠盤するから計算が速い
これってインド式掛け算てやつじゃないの？
※21
似てますね～インド式に。
マスを使うところとかそっくり。
子供もインド式で教えたらすんなり覚えましたが･･･。
でも従来式の計算方法をマスターしないと、分数（ここで躓くと先に進めなくなる）→関数→方程式への理解に繋がらなくなるから、多少難解でも従来式を推奨、と思っていたら、現実には今の小学校では筆算はもっと難解な教え方をしています。
昭和の教え方は担任いわく「指導要録にそぐわないので、昔の計算式をそのまま指導する事はできない」との事でした。
円周率も3ですしね･･･、それはもはや円じゃなくなっていると指摘をすると苦笑されました。
自分の小学生時代の理解力で左のやり方で教えられたら
掛け算するのに「引き算」「掛け算」「足し算」の3手順と
やることが多くて覚えられないと思う。
この動画は一桁目が2×5だからマシだけど、
7×6とかになってたら自分はもうヤバいですねｗ。
コーヒーや犬がいないときはどうするんだ
>>23
計算できなくなる
>>29
いや計算した後じゃんw
お茶になるとか猫と遊ぶとかにしようぜ
>>23
計算を放棄して愛犬をイメージする事に尽くす
35×12なら(35×10)＋(35×２)だけど、例えば35×18だったら普通は(35×10)＋(35×8)だろうけど、個人的に言えば(35×20)-(35×2)かな。
計算しやすい大きな数字を作ってそこから足したり引いたりする人間だらなぁ。
だから18×35だと普通は(18×30)＋(18×5)だろうだけど、俺は(20×35)-(2×35)にしちゃうけどな。
人によって”数字”の取り扱い、概念が違うからクラスで教える先生も相当技量がいるけどな。
多分クラスで8割9割は普通の計算をするだろうけど、それから外れているのが絶対にいて、”落ちこぼれ”で簡単に片付けられない現実もあるわな。
落ちこぼれも調べてみたら桁数が増えると普通の計算では引っかかるけど、スイスイと計算する”落ちこぼれ”もいるからな。
そういう意味では左の方法はちゃんと教えないといけない話だろう。
>>26
70×18して半分にすりゃいいじゃん
※107
それもあり。
その手の発想や柔軟性を持たないといけない。
その発想、柔軟性を持つためには右の計算法だけを”勉強”をしているだけは柔軟性が育たない。
ちなみに例題にした18×35を70×18にしたら拙いだろう。
18×(3５×2)/2と説明しないと…。
この桁ならどの方法でもスグだし、
桁が上がれば結局どっちでも暗算は難しい。
よってどっちでもいい
今の時代電卓の無い状況の方が珍しいしね
ぜんぶいっこずつ力尽くで計算していけば良いんだ
桁数が多くてややこしいならメモを取りながらやればいいんだ
不安なら検算すりゃいいんだ
効率が悪かろうがなんだろう、計算ってのはやるかやらないかだ
左のしてるコトは
(x+y)(p+q)
=xp+xq+yp+yq
かな？
※30
右の筆算がやってることは
xy(p+q) だね
暗算: xy・pq
右: xy・(p+q)
左: (x+y)・(p+q)
という感じで従来の方法を更に分解したということ
個人的には従来の筆算は掛ける数と掛けられる数の扱いが非対称で気持ち悪いから好きではない。左の方が数学的に合理性があると思う。
※90
＞左の方が数学的に合理性があると思う。
逆だ
3ケタの暗算やってみ
右ならできるが左は難しい
右は途中計算結果を3つだけ暗記すればいいのに
左は途中計算結果を9つ暗記する必要がある
4桁なら右は4つの暗記、左は16の暗記が必要だ
分からなければプログラム組んでみ
左は右の倍以上のステップが必要だから
※98
数学的合理性ってそういうことじゃない
小学校では、あまり抽象化しないで掛け算の意味を理解させる方に力を入れるということか。面積は具体的なイメージがあるから、分かりやすいだろうな。
しかし手間数が多いし、足し算のところで間違えるリスクもあるし、ひとつの計算で疲れてしまわないかな。
算数は得意なほうだから右のほうが手間が少なくて良いな
いや35*12=70*6=420と暗算するタイプだ
計算方法を欧米式に変えると数学力が落ちるよ
右は2桁と1桁同士の暗算が含まれてるからなぁ
なに？
行列を先にマスターさせるの？
無茶をおっしゃる
一方ロシアは電卓を使った
皮肉っぽい動画に反感を覚えたのはわかるが、因数分解とか言ってるのは文系の知ったかぶり？全く関係ないのだが
アメリカ人って引き算出来ないからなぁ
常に足し算が前提。
２６ドルの支払いに３１ドル渡すと
「はぁ？お前ばかじゃねーの？何で１ドル余計に出すんだよ」
って感じで１ドル突き返されて
２６ドル！、２７、２８，２９、３０ドル！！
と４ドル重ねて叩きつけられる。
５ドル札のおつりが欲しかったのに。
※37
フランスでも同じ目に遭ったよｗ
※37
それでお釣りがぴったりなのを見てびっくりされたって話聞いたことある
日本はチップ文化ないから小銭使わないとどんどん溜まっちゃうから皆使うし
それが当たり前だから通用するってのあるね
掛ける数、掛けられる数の両方を十の位と一の位の二つに分ける理由が分からない。
片方だけで良くないか？
どうせなら因数分解して組みなおした方が、理解が深まると思うんだが。
インド人なら暗記してるレベル
因数分解とかみたいに暗算で分解して
計算する思考は育てられるかもね
ただ単純な四則演算は素早く計算することも重要だから
一概にどちらがいいとも言えないかなあ
個人的には四則演算は単純な暗記計算でいいとは思うが
右はステップごとに意味を説明していないからそもそも比較になってない
わかりやすい！！
取っ掛かりとしては最強の教え方だわ
二桁だからやってるんだろうけど
これを四桁同士で掛け合わせたら16マス必要になる
それぞれ計算して最後にまた足し合わせる手間が非常に面倒くさい
汎用性のない計算法にわざわざ変える必要があるのかね
まあ掛け算の原理を理解するのには役立つかもしれんがそれ以上の意味はないね
※43
筆算も、やっている事は
この左のマトリックス表のうち
横一列を予め足しながら書いているだけだから、
左の理屈を理解したのち、
慣れてきたら横一列を一気にやって
（4列4段で16個の数字でなく、
1列4段で4個の数字にしておく）
筆算方式へ移行できそうな気もする。
電卓で計算したらよくない？
掛け算を足し算で処理するって方法は昔からあったよ
ただ頭の中で足し算を高速に出来る特別な人用って感じ
普通は掛け算を有る程度暗記して計算したほうが速いし
時間がかかる分、ミスが少なく、ミスに気づきやすいのは左
350+70＝420
昔のままでいいです、、。
そろばんやってたけど、こんなの０．５秒でとける。
だって頭の中で絵にするだけだから
内容的に二次関数だから余計に難しくなってんじゃね？
海外にも老害ってあるんだな
コーヒーと犬でクッソワロタw
え、これってそういう動画ですよね？
フランス式だね。
速算だな
前に本で読んだ
書かないでやると頭のトレーニングになる
つ スマホ
自分はどちらの方法でも習った記憶があるな
同じ問題に対して複数の解き方で数学の柔軟性みたいなのを学んだ気がする
最初に理解させるときは左で
あとで「早い方法」として右を教えたらええ
その前に九九の暗記
海外の反応の一番上のと同じやり方だわ
なるほどな。小学校でプログラミングを教えると言う話と連動する。昔の教育には「仕組み」と「段取り」を教える授業がなかったからな。 E テレの「デザインあ」や「ピタゴラスイッチ」みたいなの。
2ケタ(2^2=4マス)ならともかく、4ケタ(4^2=16マス)、5ケタ(5^2=25マス)になったら、収拾つかなくなる気が…
左で習っても、結局は習った通りを機械的にやるんだろうから同じような気が
この場合なら7x5x12=7×60=420が俺は一番楽かな
5×12=60は定石というか時計の針
※65
現実はそうなるし右でも理解する奴は理解するしな
でも不特定多数に教えるってなら左だろ
分割すると覚えなきゃいけない数字が増えて暗算がやりにくくなる私
暗算が得意な人は、頭の中でソロバンの珠が動いてるようですｗ
正直ソロバンだけは、すぐに辞めてしまった事を悔やんでる。
昭和のくだりw典型的なガラパゴス日本人か
両方覚えるのはいいと思う、どっちを使うかは性格次第って感じ、
ただ、どっちか一つを押し付けるのは、なんか嫌
左は右の解説。
右がオススメ。
息子の宿題を見ている時にこのやり方で解き始めたので！？となったの覚えています。
自分たちの習った右のやり方と違うので３０年以上も経てば解きかたも変わるのかと妙に感心したものです:-)
息子の宿題を見ている時にこのやり方で解き始めたので！？となったの覚えています。
自分たちの習った右のやり方と違うので３０年以上も経てば解きかたも変わるのかと妙に感心したものです:-)
インドは19×19まで九九として習うと聞いたことがある
だから計算が早いんだと
音で覚えたのは忘れにくいと聞くから、「仕組みを理解してない」九九の丸暗記もあながち馬鹿には出来ないと思う
遊ぶためには一定の基礎知識があるとやりやすいと思う
数学はおろか算数の時点で苦手意識こじらせた自分としては右が良いわ
左は、数式の意味を理解するとっかかりとしては優れてるだろうけど
たぶんあの頃の自分だったら、まず最初に大混乱する
まぁ、どちらも教えた方が良いとは思う。ただし、自分ならまず右を教えてもらってから
左がいいかな……
計算式書くのめんどいから
３５を10倍にしたのと2倍にしたの足して
答えだけ書くだわさ。
かなり昔の話だったと思うけど、小学校低学年で掛け算やってる日本おかしいってアメリカ人教師が言ってたって話があったような
英語だと計算式と数字の桁を表現する音の数が、計算式が長くなって桁が上がると音の数も多くなるから子供には覚えにくい、って理屈だったような
だから九九で覚えられる日本ずるいとかそんな趣旨だったような
>>79
なんだそれ(´ﾟдﾟ｀)
最近の教え方うらやましい、昔の教え方だと教わったもので完結
そこから発展していかない
数学的な考え方が出来るようになってたら人生楽だったろうな
昔の掛け算は「やり方」を教えているけど、今の掛け算は「どうなっているのか」を教えている、その違いじゃないですかね？
化学や物理で言ったら、授業部分(昔のやり方)と実験部分(今のやり方)みたいな、理屈を知って実際を知る感じ。
左のやり方だと、かける数が３ケタ、４ケタと増えるたびに扱う数がどんどん増える。
そっちのほうがあとで足すときに間違いやすいと思うけど・・・。
左のやり方はどうしてそうなるかの説明のときだけで、実際使うのは右のほうが
効率はいいよね。
べつに、アメリカの子供は「新しい数学」の方法しか習わないってわけじゃないんだろ？
筆算だってやるよな？
表記方法が違うだけで、原理としては両方とも同じことをやってるわけなんだから。
左の新しいやり方は面白いね
どちらかといわず、両方学んでおきたい
同じ事でも別の角度から解いてみるというのは、とてもいい脳の訓練になる
でも左は実用的ではないから、学年が進んだら右のやり方だけ使えばいい
インドだと二桁の掛け算も九九と同様暗記していると中学のとき先生に言われたな。
そこまではいらんから受験にはせめて20までの掛け算は暗記しとけと言われた。
>>85
せめてってレベルじゃない気もするが…私も今からやってみよーっと
これならもっといい方法ありそうなんやけどなあ
右で習ったから、左のやり方はまだるっこしく感じられるけど、これから学ぶ子にとってみれば左の方がわかりやすいかも
学問と問題解決・意思決定能力は分けて考えるべきだと思う。
平成生まれでも左みたいなまどろっこしいことしないぞ
左みたいな思考法が根付いて育つ人間はフェイクニュースに引っかからなくなるのか？
さらに右にGoogleの検索バーに入力、待ち時間は猫と戯れる動画を撮るべき
>35 x 10 = 350 35 x 2 = 70 350 + 70 = 420
自分もこの方法が楽ですわ
そもそも、複雑になったら電卓に頼る＝困ったらわかる人に聞くって思考に育ったので
色々手遅れなんですけどね(´・ω・`)
暗記が楽に出来るうちはどんどん詰め込んどけと思う
単純な掛け算だけならそろばん最強だし、速い。けどこれは上のコメントにもあるように因数分解とか「数学」の基礎が習えるね。
因数分解みたいだね
位上がりの小さな1とかの暗算でイラついてたけどなー
左の様な全ての計算方法を試すか覚えた上で右を最効率として覚えるのがベストだと思う。
四則演算の話で、なぜか盛り上がるコメ欄が好きです。
左を理解した上で右をやってるんだと思ってた…
状況によっては右の筆算を「70・350」じゃなくて「10・60・50・300」って書いてたわ
こういうの概念や仕組みとしては一度教えておいたほうが興味も持てていいんじゃないかな。
やみくもに計算ドリルばっかやらせるよりもいいと思う。
数学って如何に横着するかが本質だろ
基礎としてはどっちでもいいよそこから先が問題
なんとなく35x２だと70になって楽になるって直感しちゃうんだよね
数字を丸めるのが、いわゆる手癖というか・・・習い性というか
で２倍したから12も２で割ると６で計算しやすい
70x６だと420で暗算できちゃう
九九とか出来ない人だとどうなんだろうな
左の説明は掛け算を理解していない人向けの様だね。
二つの値の掛け算は長方形の面積を求める事と同じだが
普通に掛け算を理解している人や試験で解答を得る為なら
断然、右の方法を使うだろう。
要は面白いと思うけど、みんなこれを使おうと持ち上げるほどの事じゃない。
右側もちゃんと理屈があるんだぞｗ
（だからいつなるときも解が正確に求められるのであって魔法の呪文ではないｗｗｗ）
例題でいうなら「３５個セットが１２束あります」→「３５個セットが２束と１０束」
→「３５×２」＋「３５×１０」→７０＋３５０＝４２０
左側のはこの「３５個セット」をもバラバラにして説明している
３５個セットは「３０個と５個だから・・・」というふうにね
数式の「仕組みを説明する」例題として使うなら左は面白いけど実用性には欠けるね
右だって仕組みを冒涜しているわけではない上に実用的なのにどうしてここまで叩かれるのかその辺が全く理解不能
116だけど途中乱暴だったのでもう一度書き込みｗｗｗ
「３５×２」についてはそれまでにできている前提で書いている
（ちなみにオラは小学生の頃には筆算は「１桁×１桁」→「２桁×１桁」→「２桁×２桁」の順に倣った記憶があるｗ）
ここだけの縦型筆算を別で説明すると
「３５×２」→「３５は３０と５でできている」→「３０×２」＋「５×２」→「６０＋１０」＝７０
小学生の算数であっても経験が重なると自然と「１０×１０＝１００」とか「３５×２＝７０」とか「５×１４＝７０」とか「１２×１２＝１４４」とか自然に自分から「セットもの」にしていくもんだよね
いちいちそのたびに筆算などしないｗｗｗ
いずれにしても右側の計算法も決して魔法の呪文ではなく論理的だということだよｗ
たしかに小学校で掛け算の筆算習ったときのことを思い出すと
これはこういうものだからこうしましょう、っていう教え方だったように思うなあ
これはこうだからこうなります、みたいなものではなかったように思う
ただ授業の時間制限もあるから、その点から考え直さないといけない問題なのかもね
約数を知ってるなら一番早いのは
35×１２＝７×５×６×２＝（７×６）×（５×２）＝４２×１０＝４２０
わざわざ足し算混ぜるのは論理的じゃない
新しい教え方は方程式に馴染みやすい方法だとは思った。
凄いな、こういう便利なので自分がしてたのは
49×25を
50×25にして、1250として
1250－25=1225
とかいう当たり前&めんどいやつくらいだ
手順を増やしただけで、やってることは一緒やん？
左のは九九を覚えずに足し算だけで計算しましょうってことか
九九なんて小学校2年生が何日か頑張って覚えるもんだと思ってた
九九を覚えちゃいけない宗教とかあるの？
何人か書いているけど、自分も３５ｘ１２＝７０x１２／２で考えるかなー。
とりあえず一桁の掛け算なら簡単だから
このやり方って、中学以降で勉強する２次方程式
(x-2)(x+2)や(x+2)^2
を、理解するのに筋道だっていて良い教育方法だと思うけど
両方教えてあげれば良いのかな
次元軸構造準拠もいいよね、四次元以降も余裕でいけるのが強み
ただ九九(ダイレクトＤＬＬ)は便利なので暗記はした方が・・・
それに対して左はＣＰＵパワーだね、フロート用の計算プログラムって左のになるよね？
古い記事にコメントするのもあれだけど、因数分解を調べてて辿り着きました。
日本だとたすきがけでやるけど、アメリカだとAC法が主流らしい。国によってどちらを教えるのか調べたかったけど上手く調べられなかったから調べて記事にしてくれたら嬉しいです。