この画像を大きなサイズで見るシンガポールのある小学校で出題された小学1年生向け（７歳）の算数のテストが話題となっていた。大人目線だから混乱してしまうのか？もともと難易度が高いのか？なかなか回答が導き出せないというのだ。
その問題をもう一度見ていただこう
この画像を大きなサイズで見る円に記載された5つの数字のパターンから、外周にある4つの円に数字を書き込め。
問題はたったこれだけだ。とてもシンプルな問題であるが、答えはシンプルではなかったようだ。
答えが何通りもあるのである。
ネット上では様々な回答が飛び交っていた。
回答例：円が接している2桁の数字の数
この画像を大きなサイズで見る回答例：2が横にずれていることに着目
この画像を大きなサイズで見る回答例：1桁目の数字が隠れていることが推察できる
3つの円の数字の合計は、各象限の数字と等しい
この画像を大きなサイズで見る回答例：各象限の数字は、それぞれの外周の2つの円と中央の円の数字の合計に等しい。外周の円の数字は1～9までで、それぞれ1度しか使用できない。中央の円の数字から次のように4つの円の数字を求めることができる。
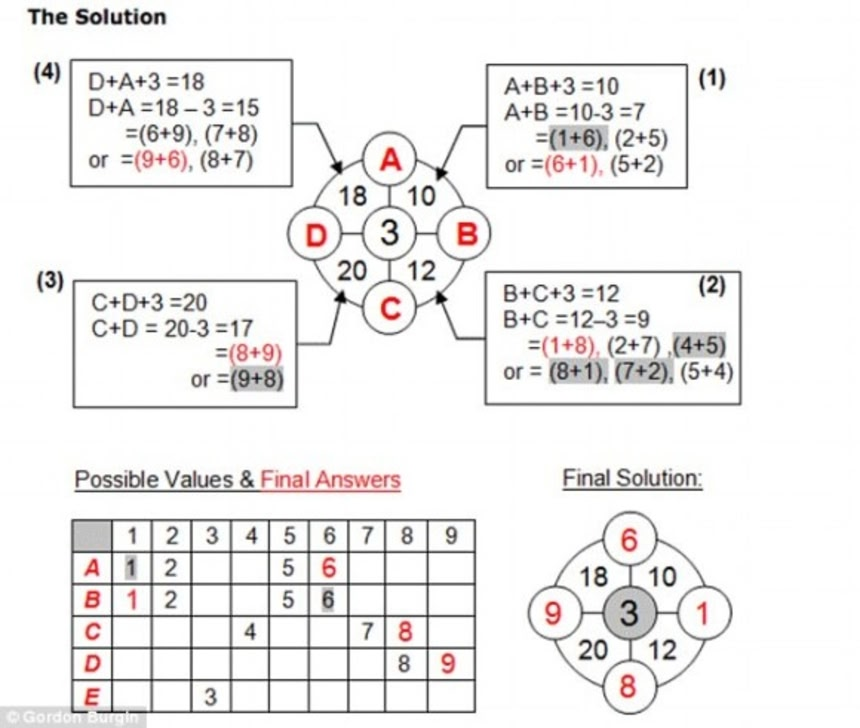この画像を大きなサイズで見るどれも正解のようであるが、情報が少なすぎるゆえに出題者が本来意図していた解答は今のところ不明だ。さて、君はどう答えを導き出した？
この画像を大きなサイズで見る難解な問題といえば、数年前シンガポールの算数問題（実際にはアジア数学五輪の問題）として話題になったものがある。こちらも大混乱を引き起こした。
この画像を大きなサイズで見るアルバートとバーナードはシェリルと友達になった。そこで彼女の誕生日を聞いてみた。するとシェリルは10種類の日付を教えてくれた。そのうちどれかが誕生日だという。
5月15日 5月16日 5月19日
6月17日 6月18日
7月14日 7月16日
8月14日 8月15日 8月17日
さらにシェリルはアルバートに何月かだけを教え
バーナードには何日かだけを別々に教えた。
アルバート：結局シェリルの誕生日は分からなかった。でもバーナードも分からなかったはずだ。
バーナード：うん、最初は分からなかった。でも今ので分かったよ。
アルバート：そうか！なら僕も今ので分かった。
さて、シェリルの誕生日は何月何日？
解答はここをクリック
via:Think you’re smarter than a first-grader?/ written hiroching / edited by parumo
2番目の問題は日本語訳が悪いと思うの。
アルバートは、「君も分からなかったはずだ」と言ってるの。
「でもバーナードも分からなかったはずだ。」っていうのはおこがましいし
「うん、最初は分からなかった。」って言葉を聞くまで選択肢は減らない。
>>2もいってるようにアルバートの最初のセリフの後段が混乱を招いてる
シェリルの誕生日は7月16日
なぜなら、
「日だけ聞いてもわからないことが明らかである」→唯一19日を持つ5、唯一18日を持つ6月ではない …( i )
「日だけ知っているものが( i )の事実を知ることで月日を特定出来る」 → 7、8月のなかで唯一の16日、7月16日である。
合ってるかな？
>>4
(i)を知る事でバーナードが答えを知る所までは分かる
でもその後アルバートが答えを知るのは何で？
最後に月を知っているアルバートが
「今のでわかった」と言ったのだから答えは一つ。
↑この部分がさっぱり理解できない
※6
「バーナードが答えを知った」こと自体がアルバートについては答えになってる。
与えられた条件で、バーナードが正しい答えにたどり着けるとしたら、答えは一つしかないわけで。
アルバートの「そうか！なら僕も今ので分かった。」は答え合わせみたいなもん。
※6
仮にアルバートが知っているのが８月だったらバーナードが15日か17日かが特定できないので『まだ分からない』と答えてるはず
それを『今ので分かった』といったのは14、16日の二択で14日が消えてる（仮に７月と８月に共通してある月14日であればバーナードはどちらの月が誕生日か特定できない）
１６日の一択のみの７月が正解ってこと
「どうやってアルバートが日程を特定出来たのか」ではなく、「まだ分からないい」と言わないのはなぜかと考えると分かりやすい
※11
19日と18日は５月と６月にしかないでしょ？
もしアルバートの知ってる誕生月が５月か６月だったら
『結局シェリルの誕生日は分からなかった。でも（１８日か１９日の情報を持っている可能性のある）バーナードは分かるかもしれない』って答えてるはずってこと
それを『分からないはず』と断言しているのは５月か６月じゃないってこと
シンガポール在住。。。今後
このレベルの算数に3歳の息子がついてゆけるのかが心配。。。もちろん私は全くわかんないw
誕生日の解答がわからんー
なぜ日付けを知ってるバーナードが分からんと言っただけで５月と６月を除外出来ちゃうの？もしかしたら15日や16日、或いは17日って教えられてるかもしれないわけで、それらの日付は他の月にもあるから、最初のバーナードの分からん発言で除外できるのは５月19日と６月18日だけじゃないか？
誰か易しく解説してけれ
※8
アルバートは最初に「バーナードも分からなかったはずだ。」って言ってる
アルバートがシェリルに教えられた月が5月か6月だった場合、もしバーナードが教えられた日が18日か19日だったらそれだけでバーナードは誕生日を知れるわけで、「バーナードも分からなかったはず」と明言することはできない。
見た瞬間、放棄したくなる問題ですね。これ、どっから攻めたらいいんだ？
私が馬鹿に思えるからやめて！
俺も和かと思ったけどなるほど”2 “を二桁と見るのね
“Fill in the missing numbers”なら訳が悪くね？
時計周りに7.11.1.5
時計の文字盤だなこりゃ
12と18はそれぞれ0と6と見れる。
12と2の間が1、対面は7。
10と12の間が11、対面が5。
真ん中の3は2と18の間が3ではない=10と12の間が9ではないって事かな？
※15が正解だろ
※53
月担当のアルバートの立場で考えれば解る。
先ず、アルバートは7月だと知っている。
5月と6月が除外されたことでバーナードは正解が解った。
7月のうち8月と日が重ならないのは7月16日しかない。
ここでアルバートも正解が解った。
正解したら50点くらい貰えるなら
必死で考えるけど1～2点なら捨て問題だな。
2がずれてるからってゼロを書き込んだら問題の前提が崩れるだろ。
そもそも左下の1桁目が削れたとして、何故0～9のうちゼロが入ると思ったんだろうか
両サイドが積、上が和、下が差、で埋めたらなんかスッキリしたから満足。
答えが出ないだろうな～と思いつつバッチリ答えがあった場合の悔しさを感じたくないから5分考えました。
大勢の人間の脳をクラウドだのグリッドコンピュータに見立てて、
「ありもしない答えの計算」をさせて「誰も考えたことのない斬新な計算法」を、
捻出させようとするがごとくだな
「できない病にかかってない？」という、ブラ企の「自己啓発」な、知恵を出す仕事を思い出すぞ。
2のところで引っかかったわ
なんで個々だけ数字が小さいのかと
バーナード「も」わからなかったはずだ、か勘違いしてた
5or6月ならそうは言えないもんな
すっきりしたぜ
問題としての価値があるの？
“（子供の学力向上の）問題”としての条件を満たしてないと思う。
実は「思考する習慣をつける訓練」が問題の意図だったりしてｗ
※23
実際そうだと思うよ。
「決められた手順に従ってアウトプットしなさい」じゃなくて、方法自体を考えるって大事だと思う。
上が22、右が16、下が8、左が14かと思ったんだけど違うかな…
正解はどうでもよく
過程が論理的であれば、それ自体が正答
7/16は普通にわかったけど最初のぜんぜんわがらん
左下が20だったら、時計回りに上から6、1、8、9で辻褄が合うのかな？
丸の数じゃだめ？
これ、普通なら内円一つ隠して外円を一つ表さないと算数の問題として成立しないんじゃ？
答えは人の数だけあるって言う創造力を養う問題ですって事なら納得
アルバートには
「君にも解らなかった“はず”だ」などと曖昧な言い方をせずに、
「君にも“絶対”解らない」と、断言して貰えると解りやすかったかな。
誕生日だけでもクッソむずいなｗｗｗ
小学生のおれは絶対解けない自信があるわ
周りの円の一つも例がでてないんだからそりゃ答えが複数になるわな
問題作った奴が馬鹿
そもそも小さな丸の中が全て空なんだから、決まった法則なんて無いわけで。
丸の数でもいいけど、それだと外の円になにいれたらいいのかわかんない
これはただ単に子供たちの想像力を試すテストなんだよ
うん、シェリルとは友達になれないことがわかった。
なんで5月と6月消えるのかわからん5月19と6月18が消えるのはわかるけど
※39
他の月に被ってない数字、19か18であれば、バーナードは自分の情報だけで誕生日を特定できる
それなのにアルバートは「もしかしたらバーナードは誕生日が分かったかもしれない」ではなく「バーナードも特定できない」と言っている
シェリルの誕生日が５月か６月だったらアルバートは19日か18日の可能性を考えて前者の発言をしている
なので５月と６月が消える
※39
自分の頭の整理も兼ねて、なるべく分かりやすい説明に挑戦してみる。
5月と6月には5月19日と6月18日という「『何日か』の情報だけで答えだと分かる日付」がある。これの持つ意味がとても大きい。
そして次に【アルバートは「5月よ」と聞いた】と仮定する。
5月には上で述べた「『何日か』の情報だけで答えだと分かる日付」が入っている。するとこの時点でのアルバートの考えはこんな風になる。
（5月19日なのかもしれない）
（もしそうならバーナードは「19日よ」と聞かされる。19日は他にないのでその情報だけで誕生日を特定できる）
（つまりバーナードには答えが分かってる可能性もある）
しかし実際にはアルバートは【でもバーナードも分からなかったはずだ。】と言っている。「バーナードには答えが分かってる可能性もある」と思ってはいない。
という事は、この仮定は誤りで、アルバートが聞いたのは「5月よ」ではない、という事になる。だから5月が丸まる除外される。同様に6月も除外できる。
うーん、分かりやすくないかも…
北が9
東が5
南が4
西が6
な、気がしました！ﾊｧｯ
円の問題はただ単に説明不足だと思います…(呆れ
何度見返しても推察は不可能、解答が複数存在するとか数学の問題としてどうなのよ。
特に答えが定まっていない問題なのかもね。
書き込んだ数字とその説明に矛盾がなければ正解っていう。
そういう学習も大事だけど小一の算数でやることなのかは疑問だな。
※45
除外できるでしょう。
アルバートが知っている月のうちどの日付が正解であっても、バーナードは日だけでは特定できない。
だが、19日は5月にしかなく、18日も6月にしかない。
よって、5、6月は除外できる。
これが第一段階。
シンガポールでは自分で考えることができる子供が育っていくのだろう
単純な足し算の問題じゃないのかな？ 円に接している数字に、あといくつたせば45になりますか？ という問題だったら、上が「17」、左が「25」、右が「23」、下が「31」でいいのでは？
仮にバーナードが15日と聞いたと仮定するなら バーナードは5月か8月と絞れる。
で「バーナードも分からなかったはずだ。」で5月と6月が消去できるなら
8月15日という答えもできるはず？
問題がおかしいとしか言えない 5月と6月を消去できないはず
※48
問題はおかしくない
なんだか混乱している人が多いけど、これはシェリルの誕生日によってはアルバートとバーナードは誕生日を特定出来ないっていう問題なんだよ
たまたま分かった、分からないの問答だけで誕生日を特定できるってだけ
仮に8月15日がシェリルの誕生日としたら
アルバート：（８月か。14日15日17日、どれも他の月にもある日付だな。日付だけでバーナードは誕生日を特定出来ないな）バーナードも分からなかったはずだ。
バーナード：（その言い方だと唯一の18、19日のある５月６月じゃないんだな。ということは残りの15日に合う月は8月だ）今ので分かったよ。
アルバート：（仮に14日ならバーナードは７月か８月かを特定出来ないはず。残りは8月15日 8月17日だが特定できないな…）僕はまだ分からない
というやり取りをしてる
これは詰みなので問題見ているこっち側も特定出来ない
だが彼らは特定できてるので8月15日 8月17日は候補から外れるってこと
※54
そうか 6月の17と被るからか、サンクス
この記事見て、
？＋？＝12
みたいな問題がたくさん並んでいるインドかどこかの数学ドリルを思い出した。
この答えになる問題はいくつもあるし、きちんと正確に理論立っていればどれも正解。
「答えは人それぞれ」で、正しいんじゃないかなこれ。
どうしても日本人脳的には1つの答えを導き出したくなるけれども。
正直なんもわからんし考えるのやめた
とりあえずシェリルが悪女的ってことだけ分かった
8月15日と8月16日をなんで除外できたのかわからない
間違えた、8月15日と8月17日をなんで除外できたのかわからない
※56
バーナードはシェリーから16日である事を聞いているので
5月16日か7月16日のどちらかってとこまでは候補をしぼれてる。
そしてアルバートの言葉で5月の可能性が消えたので7月16日の方だと分かった。
一方アルバートが聞いているのは7月だって事。
この時点でアルバートも7月14日か7月16日のどっちかという所まではしぼれる。
そして「候補から5・6月を消去しただけでバーナードが正解に達した」って事で
「7・8月の両方にある14日ではありえない」って事が新たに分かった。
よって7月16日だけが残る。
まあ空白埋めるルールからみつけなきゃいけないんじゃきついよなー
実際にはそのルールこみの問題なんじゃない？
はず って言うのが引っかかって除外できなかったんだよなぁ・・・
～なはずって確信してたら言わない気がするし
八月十七日かと思った
すでに言われてるけど
円のは答えよりも求め方を見るための問題なんだろうねこれ
２つ目の問題が超理論過ぎて解らない。
そりゃ、18と19で無いのはわかるだろうけど、何故それだけで5月6月が排除されねばならんのだ？
日だけを聞いてわからない奴をみて、14.15.16のどれかを聞いたんだなと言うのは解るが、そこからどうすれば5月6月が排除になるのかわからん。
月を聴いた奴はどう考えてるんだ？
※63
アルバートが『バーナードにも分からないはずだ』と言い切っているから
仮に５月、６月が誕生部だとして、アルバートがどう考えるか推理してみて
もし5，6月が誕生日月なら18と19日である場合バーナードは月を聞かずとも誕生日が特定出来てる
アルバートは誕生日を知らないが、５月であれば３分の１、６月であれば２分の１という高確率でバーナードが誕生日を一発で特定出来ると知っている
こんな高確率にもかかわらず「分からないはずだ」と言ったのは何でだろう？
５月か６月であればアルバートは「バーナードは分かるかも」と言わなきゃおかしい
※63
「僕が聞いたのは『7月』だ。ということはバーナードが聞いたのは『14日』『16日』のどちらかのはずだな。
どっちも他の月にもある数字だから僕だけじゃなく彼にも正解の特定は絶対不可能だ。
もしも僕が聞いたのが『5月』か『6月』だったら、バーナードは聞いたのが『18日』か『19日』で、彼の方だけはもう誕生日を特定できてるって可能性もあったんだが」
みたいな感じと思われ。
補足すると、この可能性っていうのはあくまで「アルバートにとっての可能性」ね
それも「月の情報しか知らない時点」の。
、、、こういうのを見ていると「クジラの方程式」を思い出すんだよな。何か職業能力に直結するような実用的な学問を、学校で教えのはそんなに悪い事かね？
真ん中の数字と、隣接する二つの数字を足してみる
「ある人が2から99までの2つの数を考えた。
その数の積と和をそれぞれP氏(積)とS氏(和)に伝えた。
すると二人の間で以下のような会話がなされた。
P: 2つの数は分からない。
S: 私も分からないが、あなたがそう言うのは分かっていた。
P: 分かった。
S: 私も分かった。
ではこの数はなにか。
どのようにして2つの数が分かったのか？」
という有名な問題を思い出した。
答えはこうだ・・・イヤァオ!!!
アルバート:A バーナード:B
A: B don’t know too.
これが鬼門やんな。
Bの顔見て言ってんのか
自分の情報見て言ってんのか判らん。
仮にBの顔見て言ったとすると、
答えは8/17になるで。
6/17だよねこたえは
６月17日だと思う
６月を教えられた時点では18の可能性もあるが
もう一人がわからなかったと答えたことで18日の答えはなくなった
よって17日が確定
ってのが答えかな
IQテスト系結構得意なのに最後の問題全く歯が立たなくて落ち込んだ
コメント読んでやっと理解できた…
穴埋めサッパリわからん
学校の先生はどんな模範解答を用意してるんだろう
12の補足説明でやっと5月と6月が纏めて候補から外れるって理解できた。
ありがとう、12さん。
そして、自分がかなりのアホだと気付かせてくれたこの問題に感謝は、しない。
条件が少ないからいろんな屁理屈が通りそうだけど
面白そうな回答は思い浮かばない悲しみ
もう大喜利の世界だと思う
とりあえず1問目は、両隣の数字を掛け合わせると、全て3で綺麗に割り切れるので、上が60右が40下が8左が12。これがシンプルで一番美しい解だろ。
時計でしょ。
真ん中の3は三本の針、12を上にすれば1、17、19、11が入る。
小学校１年生で掛け算はやらないだろうから正解じゃないけど・・・
上：５ 右：６ 下：１ 左：９
3*”5″=15 15-“5″=10（右上）
3*”6″=18 18-“6″=12（右下）
3*”1″=3 3-“1″=2（左下）
3*”9″=27 27-“9″=18（左上）
だと解けた
「バーナードにもわからなかったはずだ」（１８日、１９日だったらすぐに特定できているが、そうでなかったことを確認）（しかもここで自分が告げられた月が５月６月では無いので、「わからなかったはず」という言い方で、暗に断定、密告している）
バーナードは、先のアルバート発言により、５月、６月ではなく、７月か８月であることを察知した。その瞬間に誕生日が特定できたということは、１４日ではなく、７月１６、８月１５、８月１７のどれかである。アルバートが８月と聞かされていたなら、この時点でもアルバートだけは誕生日を特定できなかったはずだが、７月と聞かされていたので、７月１６日をアルバートも特定することができた。
日付だけではわからなかっただろう
→もしアルバート側が5、6月なら、答えがひとつしかない「18」「19」が含まれている月なので『(日付だけで）君はわかったかもしれない』と言う。しかし、わからないとあるので
アルバートが聞いたのは7、8月のどちらかである。
あとは解答に同じ
え、まって。
最後のやつは日付サイドはわかったとしても
月サイドはわからんくね？
8月のふたつだとしてもバーナードは「わかった」って言えるじゃん
あぁ、コメント欄みてわかった。
アルバートの最後の「わかった」ってのはそういうことね。
名前を!アルバートとバーナードじゃ無くて、夜神月とLにすべき（笑）
特にアルバートの論理的思考能力が異常過ぎる（笑）
5月、6月の日付には一種類だけの「18」「19」があり、そのふたつが答えなら
バーナードひとりで「わかった」となる。
しかし、月を知るアルバートが
「わからないはずだ」といった。そのセリフを言い換えると「ひとりだけではわからない｣といえる。上記のとおり5月、６月は ひとりでもわかるかもしれないので除外される。
つまり答えは7月、8月のどちらか。
日付だけのバーナードが7月、8月だけが残った状態のときすでにでわかったので
まず重複している「14」は除外され、
残るは7月16日、8月15日、8月17日。
アルバートは7月か8月かを知っているので
アルバートの「わかった」は、月だけで判断できたもの、つまり7月である。
(そうか！なら今ので僕もわかった。
の【なら】は答えが３種類に絞られたこと。
そのなかで8月である場合、
「そうか。なら僕はわからない」となる。）
よって7月16日。
アルバートの「わかった」が答えの決め手。
二番目のは会話としての文だから多少は目を瞑りなよ
問題とは関係ないけど分からないはずだの後にわかったよって答えるパターンもあり得るのだからさ
一番の問題は多分最初の答えで合ってるな
必死に計算するだけじゃ問題は解けないよって事じゃないかな
2で理解出来たわ成る程ね
シンガポールの小学校のは丸の数では
真ん中は18 10 2 12の組み合わせなんめ3
左は18 2の組み合わせで2
上は18 10の組み合わせで3
右は10 12の組み合わせで1
下は2 12の組み合わせで0
シンガポールのやつ、実際は凄く簡単な答えです
該当する部分にある二桁の数字の数です
真ん中は４つ全部で見るので3
上は上半分だけみるので2
右は右半分でみるので2
下は下半分でみるので1
左は左半分でみるので1
だそうです
http://www.fullyu.com/ueditor/php/upload/image/20170531/1496192063325082.jpg
ヒントは、一年生の問題だから
かけ算わり算は使わないのが前提ってところか。
18を真ん中の3で割って6
12を3で割って4
18の両脇の○に6、12の両脇の○に4を入れる
2の表示部分は引き算、両脇の○に入っている6から4を引いて2
10の表示部分は足算、両脇の○に入っている6に4を足して10
答えは時計回りに上6右4下4左6
な～んて無理矢理当てはめても数字が合ってしまいました。
＊88で正解が紹介されてましたが、色んな答えが出せるのでは良い問題ではありませんね。
教育には、技術(必然的に確保されようとするもの)よりリテラシー(社会の問題を成立させる偏見の固定化の可否を決める)
の方が圧倒的に社会として重要だと思う
私の回答
上：19 右：13 下：5 左：11
マイナスを使わないと考えて、小さい数から大きい数の方向のみを考慮します。
上方向は、左下の２から左上に16を加えて18になっているので、3に16足して19
右方向は、左下の2から右下に10を加えて12になっているので、3に10足して13
下方向は、右上の10から右下に2を加えて12になっているので、3に2を足して5
左方向は、右上の10から左上に8を加えて18になっているので、3に8を足して11
ちなみに、斜め方向も見ると、
左下の2から右上の10の斜め右上方向に8増えていますが、
左：11に8を足すと上：19になり、下：5に8を足すと右：13になります。
右下の12から左上の18の斜め左上方向に6増えていますが、
右：13に6を足すと上：19になり、下：5に6を足す左：11になります。
どうでしょう？あ～ぁ、答え知りたい！
お互いに月と日にち教えあったらええねん
とりあえず頭がいたい
まず学年を考えて足し算しかしない事にする
中央の3は対面している2数の関係から導かれるとすれば、10＋2＝12、18＋12＝30
各位の数を足し合わせるとともに3
同様に、空白の各円をそれぞれ隣接する2数の和から求めれば上から時計回りに
1(18＋10＝28、2＋8＝10、1＋0＝1)、
4(10＋12＝22、2＋2＝4)、
5(2＋12＝14、1＋4＝5)、
2(18＋2＝20、2＋0＝2)となる
実際に図に書き込めばわかるけど1から5までの数が綺麗に収まる
計算も単純だしこれが正解かなぁ