 この画像を大きなサイズで見る
この画像を大きなサイズで見る多くの子どもにとって憂鬱な宿題。それは昔も今も変わらないが、最近の子どもと監督役である保護者たちはネット上で多くの同胞と宿題への不満を分かち合えるようになった。
そんな中、海外の育児系掲示板でシェアされた8歳児の問題が「ありえない」と物議をかもしていた。
当の子どもだけでなく親たちをも困惑させた算数の問題。それは一体どんな内容だったのか?
8歳超えてっから楽勝だし!って人も試しにやってみてはどうだろう。
助けを求める保護者がシェアした子どもの宿題
ニュージーランドのメディアサイトoversixtyによると、今年5月にイギリスの育児系サイトMumsnetの掲示板で子どもの宿題が話題になっていたという。
それは8歳の子を持つユーザーlucysmamのこんなコメントから始まった。
lucysmam:
子どもの宿題にちょっと頭を悩ませています。解けるはずなんだけど…説明できる方がいたらお願いします!
すると、奇遇にも別のユーザーも同じ問題で困惑していたことが判明。それは以下のようなものだ。答えは保護者の反応後にお伝えするのでまずトライだ。
 この画像を大きなサイズで見る
この画像を大きなサイズで見る【灯台】ある海岸に灯台が3つあります。
1つ目の灯台のライトは3秒間光って3秒間消えます。
2つ目の灯台のライトは4秒間光って4秒間消えます。
3つ目の灯台のライトは5秒間光って5秒間消えます。
なお、最初はすべての灯台のライトを同時に点灯させるものとする。
以下の問題に答えなさい。
問1. すべての灯台のライトが最初に消えるのはいつですか?
問2. すべての灯台のライトが次に同時に点灯するのはいつですか?
image credit:mumsnet
さて、答え出たかな?あと、もし子どもに解かせるとしたら、どんな教え方がいいだろう?そのへんも考えてみて欲しい。
答えは合ってる?解き方は?親御さんたちの反応
この件について掲示板ではこんな意見が交わされていた。
保護者の反応:
AjasLipstick:
これって子どもにはありえない問題よね、私も同じ状況よ。良い解き方を知ってる人を待ってるわBr1ll1ant:
ライトの点滅周期を紙に書かせて図にすればいいよMissReginaPhilange:
最初の質問はスイッチを入れた時だと思う。2番目の質問は今苦戦してるとこBalloonFlowers:
これは役に立つ?(図から6秒で全消灯。25秒で全部点灯)この画像を大きなサイズで見る
MyfanwyMontez:
うちの子8歳だけどこんなの解けないわBettyfoodWed:
何をテストする問題なのかな?忍耐力?
image credit:mumsnet
で、そろそろ答いってみよう。
最終的に掲示板の親たちは
問1. 6秒後
問2. 120秒後
という結論に至った。
以下は保護者の解説に略図もつけたので、解けなかった人は参考にするだよ。
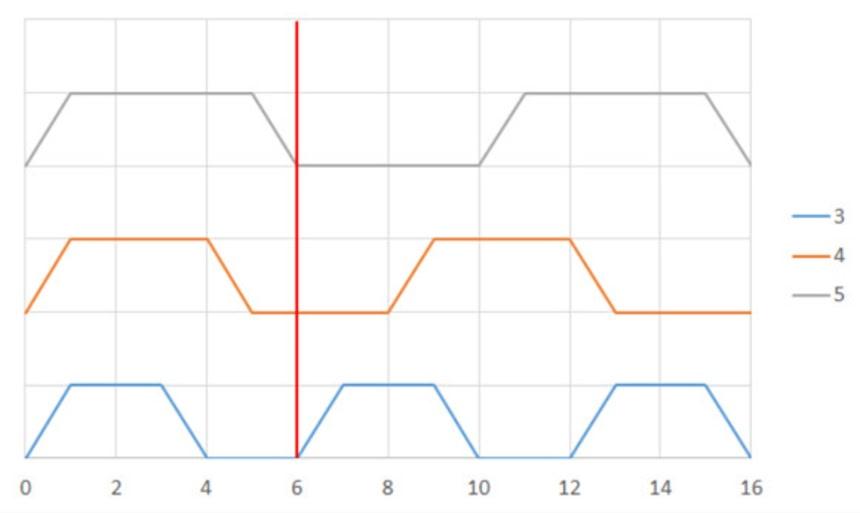
いずれもライトの点滅感覚に頭を巡らせれば解けるが、問1は、1つ目の灯台が次に光る直前と3つ目の灯台が消えた時だ。
 この画像を大きなサイズで見る
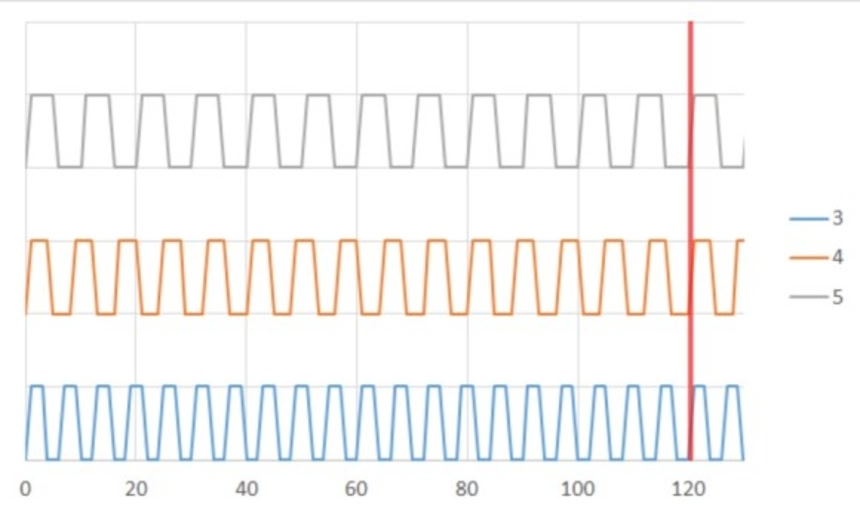
この画像を大きなサイズで見る次に問2は、ライトが光るタイミングに着目。1つ目は6秒ごとに光り、2つ目は8秒、3つ目は10秒ごとだ。
そして、次回3つの灯台が一斉に点灯する時間を求めるため、6、8、10で割り切れる最小の数、つまり(各数を素因数分解して)最小公倍数を算出した。
6 = 2×3、8 = 2×2×2、10 = 2×5 これより 2x2x2x3x5 = 120
(ただし、これはすぐ点灯する前提での計算なので細かく言えば120秒過ぎともいえるだろう)
 この画像を大きなサイズで見る
この画像を大きなサイズで見る子どもがどう解く?めんどくさすぎるでしょ!
とはいえ、相手は子どもだ。保護者の話からしてイギリスでもその年齢ではほとんどが最小公倍数を習ってないらしい(日本では小学校高学年で習うようだ)。
そこで、子どもには図で解かせたほうがいいという意見が多かった。
ただ、図にしても2番を解くには結構な時間がかかるし、途中で間違えることもある。コメントのように根気を試すテストには最適かもだが、ちょっと無理があるのではなかろうか。
てなわけで、たとえ答えを知る大人が教えるにしても8歳の子にとっては「ひどすぎる問題!」という意見が噴出していた。
保護者の中にも迷ったり、質問をうっかり読み間違えてしまった人もちらほらいたようだけど、みんなはすんなり解けただろうか?
References:mentalfloss / mumsnet / oversixtyなど /written by D/ edited by parumo
















ある意味、理解力と問題解決方法を養う問題ではあると思うw
最小公倍数を小学生でやったか忘れたけど、
地道に数えれば解ける問題の気がしないでもない
※2
3,4,5,の公倍数じゃ、3は点灯するけど、4は消えるとかになる可能性があんじゃね?
6,8,10の公倍数じゃ、同時に消えるのか、、同時に点灯するのかわかんないし、多分一回目じゃない。
最小公倍数とかの問題なんだろうけど
図を書かないと解けない
特に公式が必要なわけでもない、頭の体操に良い問題だな
解けるけど、8歳の子には難しそうだね。
1番、普段から図に描いてる子なら、思いつきそう。
最小公倍数を知ってれば何となくこうかな~でわかりそうな問題ではあるけどね
ただどうやって教えるかはすごく難しい
子供にこれは最小公倍数の問題で~って教えるとふーんで終わる
パターンとして教えるのなら覚えとけよで終わりかもしれんけど、理屈を教えてそれを最小公倍数に結びつけるにはそれなりに教え方を考えないといけないと思う
6秒は解せぬ
消えてる判定なら
120秒は消えてる判定だろ
グラフの問題?
簡単なスケジューリングを子供の内からやらせて頭を柔らかくしようとでも思ったんだろうか・・・
掲示板の親たちの回答だと、on,offに1秒かかるという条件が付加されているが、実はそういう質問なの?
日本語だと「同時に点灯する時」と「全部が点灯する時」の使い分けがアレ。
すべての灯台のライトが次に同時に点灯するのはいつですか?
これの意味の受け取り方で答えが変わるね
問2、25秒で「全部点灯」するのに?と思ったら「同時に点灯」か
暗算でパットやるのはきつい。
でも解決方法を考えさせるいい問題ではあると思う
数さえ数えられれば図を描いたり地道に数えたりして子供でもなんとか回答できる
子供同士で解き方をディスカッションさせても良さそう
121が答えじゃないのかな
最小公倍数だけでやろとするとまちがえるなw
図で確認しながらでないと
5秒で消えるなら問1は5秒後なんじゃないかと
問2は32秒後
同時に点灯ってのが紛らわしいな
地道でまあまあ簡単なやり方としては3つ目の灯台の10秒単位区切りで数を羅列していく。
次に2つ目の灯台の8秒区切りの数を出していって10秒区切りと一致する数を出していく、
最後に1つ目の灯台の6秒区切り数で一致していく数を探していく。
これなら8歳でもなんとか・・・?どうだろう
5秒後じゃないの?
6秒後には初めの3が光りはじめるやん
因みに日本では小四で習う範囲
確かに難しいね 図を書くと分かり易いと言う人がいるけど教える時は図解はしないからね
参考にするだよ、でわろた
ところで開始6秒で消灯はいいのに開始25秒はなぜダメなのかわからん。もう少し考えてみるか
最初に同時に消えるのはいつ?
※24
無い。
すべての灯台が消えている時間はあるが、同時に点灯からオフになる瞬間は無い。
※106
偶数*奇数は偶数、奇数*奇数は奇数 4比が永遠に揃わない
無いんだね、これは直感と違うところだった
この問題はイギリスに限って重要なものと言えるね
これはエイダ女史に対する敬意なんだろうと思う
図を描いてみれば、そこにミシン目が現われるから気付くね
余所者がケチをつけるのは良くない!
わからんと書いたもんだが謎が解けた、同時に点灯するタイミングってのを見落としてた
8歳というと2年生か3年生かな
1番はともかく2番は素因数分解はいらないけど最小公倍数はあったほうが解きやすいね
なくても図でなんとかなるけど
まぁたまには背伸びした問題が一つくらいあってもいいんじゃない?
ひらめいて解ける子もいるわけだし
小学生なら具体的なイメージでものを考える練習は必要
手を動かして作業するのも大切
とりあえず何周期かでも図を描いてみてから考えるといいね
全部頭の中でやるのがいいと思い込んでる子がいる(そう教える大人がいるのか?)けど
そうじゃないと教えてあげた方がいい
最小公倍数が出てこなかったわ、灯台もと暗しだな。
おれの劣等感を刺激しないでくれ
8歳には厳しいかもしれないけど、有名中学の受験くらいなら出そうな問題ではあるな、と思ってしまう。
これ何が面白いって、ただ出ている数字の公倍数の問題じゃなくて、「点く」「消える」を意識した公倍数ってのが面白いし、一問目は「公倍数で解こうとすると引っかかる」ってのがミソだよね。
問1は5秒後(Cの灯台が消えた時点で同時にABの灯台も消えているから)
問2は「同時に点灯するタイミング」だから、6と8の公倍数かつ10刻みの数字になるから120秒後
という考え方で良いのかな?
図を描いて考えるとわかるけど、最初に全てのライトが消えるのは5秒後。
最初に全てのライトが同時に点灯「している」のは24秒後。
最初に全てのライトが同時に点灯「し始める」のは120秒後。
これが答えじゃないの?
※33
そう、「同時に点灯する」を「同時に点灯している状態になる」と思ってしまうと24秒なのよね。保護者で図を書いている人と同じ。
因数分解やら最小公倍数やらは中学で習った気がするんだけど…
8才に何を使って解かせようとしたのか気になる
問1. すべての灯台のライトが最初に消えるのは
A. 最初
問2. すべての灯台のライトが次に同時に点灯するのは
A. 6秒
文系俺、勉強した最小公倍数が初めて役に立って感動
もう今後の人生で必要になることはないかもしれない
問1が6秒後って・・・
俺の捉え方がおかしいのかもしれないけど5秒後じゃないの?
3つ目の灯台は5秒後に消えるんでしょ?
「島唄」の図解を思い出した
長い紙があれば根気でなんとか…
5秒後と24秒後では?
というか、彼らの図がおかしい気がする。
一つ目の図は0の概念が無いし、下二つの図は何故台形状にする?
灯滅に1秒要すると考えてるのか?
※40
お前の言い分だと5秒以上6秒未満なだけ
電子回路は大体20msのサイクルでどこからを消灯と取るかによるけど、光量がゼロとする場合のかかる時間は1秒どころじゃないし、スイッチが入った瞬間だとしても回路が一巡20ms、最大39ms、その後に物理的にマグネットが入る時間がいる
と、物理的な話をしたところでそもそもが前提有りきの数学
少数を扱わず不確定要素を考慮しない問題の場合、5を超えた時点で6と扱うしかない
※48
問題文ではどう考えても点滅周期が6秒、8秒、10秒と考えられる。
したがって、最初の問題は5秒が正しい。
点滅に要する時間の考慮は問題文にない。
2番目の問題は考えてないので、1番目を5秒と考えた人のどれかが正しい
※78様
よくぞ仰って下さいました!
こういう方ばっかりなら、世にイジメは存在しないのに。
同時に消えるのは6秒後。同時に点灯するのは25秒後。
国語力なくて点灯の意味を履き違えた結果、24秒になったw
これはもしや・・・
転生者を炙り出すための罠?(ラノベ脳)
5秒とか言ってる奴ら大丈夫か?
後ろの問題は、英文を見ると同時に明かりがつく時間だから、6と8と10の最小公倍数でいいね。
今はどうかしらんけど、昔は小学校3年生ぐらいで習った気がする。
前の問題は、5秒分の図か表を書くだけなので簡単だろう。
同時に消灯するだと、ちと説明が面倒だろうね、ちょっと変わった旅人算だとでも思えばいいのだけれど、なぜそう考えればいいのか8歳の子供に理解させるのは面倒そうだなあ。そこそこのレベルの中学の入試に使えそうな問題だし。
5秒後はまだついてるでしょ
4秒が終わってその直後に消えたら4秒間しかついてなかったことになる
5秒になってから6秒に切り替わる瞬間までつき続けている
それと6秒が終わって7秒が始まるまでは1つ目は消え続けている
初期状態が分からないと思ったけど、問2で「次に」と言っているから0秒の時点で3つとも点灯し始めたと考えていいんですかね
※49 ※95
初期状態は「最初はすべての灯台のライトを同時に点灯させる」で、問2は「次に」だから、答え「0秒」は無しだと思います。
中学受験で出る「周期算」ってのを使えば小学生でも解けるけど最小公倍数の概念も必要だし、小4~小5くらいでやる問題
8歳ならやっぱり根気よく図で考えるんだろうね
いや、問題文が正しければ問2の正解は0秒っしょ
子どもにそんな難しい問題は解かせないはずだし
5秒後 24秒後じゃないの?
算数のテストの裏にこういう問題あるよね
頭の回転が必要な難しめの問題だけど配点は0点だから解いても解かなくても良い
解けると答え合わせの時に褒められる
これのおかげで算数好きになった
覚えてるのでは
『コイン袋が10袋ありそれぞれにランダムな枚数のコインが入っている。コインは1枚10グラムだがその中で1袋だけ11グラムのコインだけが入った袋がある。量りを1回だけ使ってどの袋が11グラムのコインの袋か調べよ。』
※53
1つ目の袋からはコインを1枚、
2つ目の袋からはコインを2枚、
(中略)
9つ目の袋からはコインを9枚、
10個目の袋からはコインを10枚
合計55枚のコインを用意し、量りに載せる。
コインは1枚10グラムなので、本来は550グラムになるはずだが
11グラムの袋から出したコインの枚数分重さが加わるので
1の位の数でどの袋のコインが11グラムなのかわかる。
551グラムなら、1枚取り出した1つ目の袋
555グラムなら、5枚取り出した5つ目の袋
560グラムなら、10枚取り出した10個目の袋
6秒後というか6秒目だよね
同時に点灯もそうだけど、翻訳がややこしい
問1 俺の希望の灯を消すことはできないぜ ?
問2 ゆこう ! 俺たちの心が一つになった瞬間だ !
これは良い問題だと思う
普段使わない頭を回転させられるし
答えは難問だけど問題自体はシンプルだからテストが終わった後
生徒同士で解き方を相談できる、良い問題
同時に点灯するのが120秒後ってのは導き出せたが最初に三つとも消えるってやつが同時になのか全部消えてたら良いのかの判断に困るな
Cは5秒後に点灯状態と消灯を併せ持つ
これをどう捉えるかによって答えは変わる
何故か60という数字が出てきた
3と4と5が一番初めに割れる数
※59
3,4,5を使うとonとoffがずれるから、かならずonになる6,8,10を使うんだよね
何秒時点なのか何秒後なのかで答えの秒数が変わってくるんじゃないかな、やるべきは図に起こした後辞典を引くことだと思う。以下と未満の違いみたいなニュアンスで答えがずれる
答えを出すのと、理解するのは別であると云うこと
子供に「何でそうなるのか」理解させようとすると大人が悩むな
ONOFF切り替えに要する1秒はどこから来たんだ
数学の計算なら0秒で切り替わると考えるはずだが向こうだと暗黙の了解なんだろうか
難しい問題を出して知能の高い子にいい点数をつけさせる問題なんじゃないの
みんなに百点取らせる気は無いんじゃない
図を書くの前提じゃねえのこれ
6秒後はすぐに分かるんだが、全点灯はちゃんと計算しないと無理
すぐに点灯しないというのがミソだな
元リンクに写真の投稿者が画像で見切れている問題文は、
first time they will all be off, and next time they will all come on together.
だって補足してるね。
ほんで、be on (点灯している)なら25秒で、 come on (点灯しはじめる)なら 120秒が正解だって書いてる人もいるね。
あと、答えは、6秒後と120秒後ではなくて、
5秒後と120秒後、もしくは、6秒目と121秒目、だと思うよ。
そう考えると be on だったなら、25秒後じゃなくて25秒目じゃないかな。
この問題作った人間がまず国語の勉強から始めないといけないな
答えは「そんな灯台は無い」
「灯台のライトON-OFFには1秒かかる」
イギリスでは8歳児でも常識なのか?
問1が、5秒後。
問2が、24秒後。
ですよ。
5<x≦6
を5秒ととらえるか6秒目ととらえるか
5.0秒経過時点ですべて消えるから5秒だと思うけど
6秒目だと6.0秒も含まれてその時点から3秒灯台が点灯するでしょ
おまえら凄いな、俺は秒速で考えることを放棄したわ
天才ってこういうの紙に書かなくてもすぐパッと視覚的にイメージして周期を割り出すんだろうな
こうゆう問題出てくると決まってマウンティングチェリーボーイが湧くわ湧くわwww
まず問題が解けるか以前に子供が設問の文章や要求されてることを理解できるかどうかがかなり怪しい
元の問題文全部見ても消灯シークエンスに1秒かかるなんてどこにも書いてないよな
全て消灯状態になるのは 5秒後で合ってると思う (元のサイトでは5秒後だろとのコメもある)
ちなみに同時に消灯シーケンスに入るのは 60秒後 (3,4,5 の公倍数)
※77 自己レス
> ちなみに同時に消灯シーケンスに入るのは 60秒後 (3,4,5 の公倍数)
今気づいたけどこれ間違いだった。
3 x 奇数C = 4 x 奇数B = 5 x 奇数C
となる必要があるけど、偶数=奇数 となる組み合わせはあり得ない。
どんだけ待っても「同時に消灯シーケンスに入ることはない」 が正しい。
いや、これ最小公倍数の問題じゃないでしょ普通に考えて
だって3つついた状態になんの25秒後だもの
最小公倍数の問題だったら3秒毎に落ちる水滴、4秒毎に~とかやるはず
3秒間ついてる、4秒間ついてる、とか紛らわしすぎ
この問題は図にして考えてみようの巻、でしょ
8歳相手なんだし
無理。
こんな問題出された日には、アタシゃ0点だよ。
あー、小学生ガキンチョの頃、1人だけ問題が解けず0点取って、同級生に散々笑われてからかわれて、学校中に触れ回られて、学校中の生徒から馬鹿にされて、いじめられたトラウマ思い出した。
今だって解けないよ。でも解けなくても、日常
なんのさしさわりもなく生きてられるんですけど。
灯台は電気点けっぱなしですが・・・。
数弱だけどなんとなく最小公倍数絡みかなとは思った
しかしそれを求めるやり方を1%も覚えてなくて絶望した
最小公倍数って小学校だっけ?中学で習ったような気がしたけど。
日本だと中堅の中学受験問題レベルかな?と思うけど
いずれにしても8歳でこれをすんなり解いたらガウスかよって思う
最小公倍数だろうけど、かなり複雑な計算がいるぞ。
8歳て、小学2年生だよねー・・
なんでもっと、算数が苦手な子や、勉強が遅れがちな子や、解くのに時間が掛かる子でも、単純明快で楽しくなる様な問題解かせないのかねえ?
数学の問題において点灯・消灯する時間を斜めの線で表すのは要素が多すぎる
この場合は瞬間的について瞬間的に消える前提のグラフを描くべき
「同時に」という言葉が問1になくて問2にはあるんだから
問1は「すべてが消灯状態にある」問2は「すべてが点灯状態にうつる」
と考えるのが自然でしょ
なんにせよ、問1=6秒はない
普通に表書いて解かせるのが目的だろう
5秒後と120秒後じゃない?
なんでか表では点灯と消灯に1秒もかかることになってるけども
6秒後ってなんやねん
同時に点灯するか、3つが点灯しているときかでも変わるな
数学が得意分野の人は解くの楽しそう。というわけで各々「得意分野の方に任せ」するのが正解☆
二問目の質問に、ゼロ秒と答えられる人は
凄くいい発想だと思う。
個人的に目からウロコだった。
日本語の解釈だと5秒後だけど
英語の細かいニュアンスがわからんから何とも
勉強に遅れがある子がいるのはわかるけど、理解が早くて暇してる子もいるからこういう問題はいいと思う
これを解けなかったからといってダメということにはならんだろうし、できた子は満足感があるしバランスがいい
本分が分らないけれど、先生の出題選択のミスでしょ
最小公倍数の問題なら
同時に点く時は、3と4と5の最小公倍数
同時に消える時は、その倍数の6と8と10の最小公倍数なんだけど
基本的に、灯台は点滅しないから
2重3重に問題自体がおかしいんだよね
船の進行速度と其々の灯台の角度の関係で
光っていると感じる長さも変わってくるからね
※98
そりゃあなた、等速で直線上を移動する点Pだとか、なぜか同時に家を出発しない兄弟だとか、同時に出発点に到着するまで何度追い抜いても池を回り続ける二人とか、算数の問題にツッコミを入れだすとキリがないでしょ
これ図を描けばめんどくさい数学を使って解く必要はないんじゃないかな
知ってる分大人は公式を使ってスマートに解くのが正しい、それ以外の解き方はしてはならないと思い込んでいるけど
図に描くことで視覚的に算数の仕組みを理解させるとか子供の発想力を発揮させることを出題者は望んでるんじゃないかな
割り算を習ってない幼児でもおはじきなどを使えば結果的に割り算と同じ答えを出せるように
ヤバい
まず慌てて問題の意味を取り違えてアウトになりそうだわ
いっせーのせで同時に点灯するってのと、全て点灯してる状態ってのと(消灯も同じ)
これ、工業系の大学で出したらもめるな。
スイッチングで。
3秒で消灯するなら3.000秒の瞬間はオン?オフ?
同様に6.000秒の瞬間はオフ?オン?
「3秒”間”」と設定されていて「3秒”後”」じゃない。
なぜ25秒でないのかどうしてもわからない
※104
注記がない場合は点消灯にかかる物理的な障碍は一切無視してその秒に至った瞬間に「一瞬で」切り替わると解釈すべき
10進数かどうか明記されていないから答えられないというのと同じレベルの揚げ足取り
※108
工業大学だともめるだろう
と言っているだけでなぜ揚げ足取りになるかわからない。
条件が書いてないとか質問者が悪いとかケチつけてる
わけではないのに。
全部のライトが同時に消灯/点灯するときであるのか、全部のライトが消灯/点灯された状態になったときであるのかが不明瞭である。
息子が解けて自分解けなかった……こんなとき、『天才!』ってほめる以外にどんな顔したらいいかわからないの。
図を描くってのは数式の意味を理解するってことだと思う。
点灯・消灯にかかる時間はかからないとして。3・4・5それぞれの奇数倍に当たる時間で消灯、偶数倍で点灯するのだから・・・む~(´・ω・`)
三番目の灯台の点灯時間は0<X≦5、消灯時間は5<X≦10なので、
5.0秒ではまだ点灯状態なんじゃないかな。
同様に一番目の灯台の点灯時間は0<X≦3、消灯時間は3<X≦6なので、
6.0秒はぎりぎり消灯状態ですね。
朝になったらとか夜になったらとかそういうのだと思ってたら違った
8歳だって時間さえかければ解けるだろう
そんなに悪い問題だとは思わないけど
文句言ってる親は自分が解けないのが面白くないだけでしょう
なんつうかまあ悪問ってことでいいんでないかな
算数の宿題あるあるだよね;
答えはわかるけど、教え方と導き方がわからないっていう逆の問題さ;
マイナスや分数、記号を使えないのにどう説明しろと?ってのが何度もある
答えはあってるのに、証明の仕方が違うって「×」がついて帰ってきたりさー
(教えた内容を理解しているか、てとこを見てるんだろうけど)
この記事だと表にしてあるのはわかりやすくていいな
問題はこれをテスト用紙に書いて、正解をくれるのかどうかってとこ
一見して最小公倍数じゃんとか思って解こうとすると混乱するな
120は図で地道に解こうとすると途中でこの方法で合ってるのかちょっと不安になってくる数の大きさ
なぜ最初が揃っている前提なのか
結論:光っている時間が
0 <= x < 3 なのか 0 <= x <= 3 なのか、 0 < x <= 3 なのか等で答えが変わる。
8歳なら日本人でも習わないよ。小5からだから10歳頃のはず。8歳はまだ小2,3。カラパイアさんはたまに英語訳を間違えるから元ネタを見てきた。
5秒に注目をすればいいかな?
1)6秒(5秒のがoffになる時)
2)12秒(3秒と5秒が同時についてる時。’on in the same moment’英語の元ネタの方のニュアンスだと同時にパッとつくのではなくて、全部ついてる状態とも読めますから。だから3回目の3秒がonになれば全部同時にonの状態になるはずだが)
8歳の問題から複雑に考えるようにできてると思わない。
※あくまでも個人的に思ったことです。
全消灯は6秒でいいとして、全灯は0秒じゃね?
アナログ的に、オンを〇/オフを×として、右に右に表を書いていけば合ってるみたいだけど、やっぱり120は不安になる長さ…。25だと思ったんだけどなあ。グラフのナナメの線はまぎらわしい。
5
120
以外はない
勝手に条件付加する奴大杉
そんなに騒ぐほど難しいかな?
2問目は計算すればすぐ分かるし、1問目は図を書けば分かる。
(すっかり忘れてる)大人より、子供(しかも授業について行けてる子)の方が解けそう。
親に聞かないで解けてる子は多そう。
親に聞いているような子供は授業についていけてないのでしょう。
2問目の大人の回答は「同時に点灯し始めるのはいつか」で120秒(120秒経過後)
一方で25秒(24秒経過後)というのは「同時に点灯した状態になるのはいつか」だな
原文が英語なのでニュアンスがわからんが、翻訳した通りに受け取るなら後者のような気もする
5秒後と0秒じゃないの?
読めば読むほどわからない
文字通りなら
1は明るくなったら、2は暗くなったらとかじゃないの?